Seja a função definida pelo gráfico:
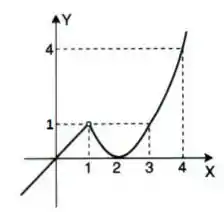
Intuitivamente, encontre se existir:
e)
Passo 1
Eaee, belezinha?? Bom... O enunciado nos deu o seguinte gráfico:
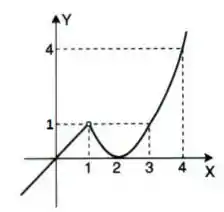
Queremos verificar se o seguinte limite existe:
Para verificar se o limite de existe em , devemos analisar se os valores de convergem para o mesmo número quando se aproxima de pela esquerda () e pela direita (); se sim, o limite existe e vale , caso contrário, não existe.
Passo 2
Para pela esquerda, temos que a função tende a , certo? ? A fim de facilitar a visualização, vamos desenhar uma seta para mostrar por onde os números estão vindo, saca só:
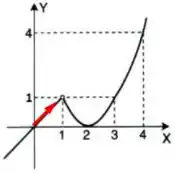
Para pela direita também temos que a função tende a , não é mesmo? Assim como fizemos para pela esquerda, vamos desenhar uma seta para mostrar por onde os números estão vindo, se liga:
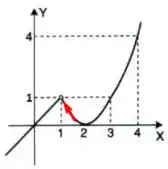
Note que as setas estão apontando para o mesmo ponto em comum, que está em . Quando os limites laterais dão iguais, como é o nosso caso, então o limite no ponto existe e vale o mesmo que esses limites laterais. Como nossos limites laterais se aproximaram de , então podemos concluir que:
E esse é o nosso resultado!