Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.7 - Ex. 3
Uma partícula move-se segunda a lei do movimento , , em que é medido em segundos e em metros
- Encontre a velocidade no instante
- Qual a velocidade depois de
- Quando a partícula está em repouso?
- Quando a partícula está se movendo no sentido positivo?
- Encontre a distância total percorrida durante os 8 primeiros segundos
- Desenhe um diagrama como na figura 2 para ilustrar o movimento da partícula
- Encontre a aceleração no instante e depois de
- Faça os gráficos das funções posição, velocidade e aceleração para
- Quando a partícula está acelerando? Quando está freando?
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função posição de uma partícula
E nosso objetivo é a partir dela encontrar uma série de coisas: A função velocidade, a velocidade em , quando a partícula está em repolso, quando o movimento da partícula é positivo, a distancia percorrida no intervalo de , encontrar a função aceleração, esboçar os gráficos da posição, velocidade e aceleração, encontrar a aceleração em e por fim determinar o intervalo de tempo quando a partícula está acelerando e quando a partícula está freiando.
É muita coisa, não é?
Bom... para resolver esse problema temos que lembrar dos princípios físicos que diz que a velocidade é a variação da posição sobre a variação no tempo
E a aceleração é a variação da velocidade sobre a variação do tempo.
Trazendo isso para a nossa realidade, taxa de variação é a mesma coisa que derivada em um função, ou seja
Então derivando a função vamos obter a função velocidade e derivando a função velocidade, vamos obter a função aceleração...
Veja só!
Passo 2
Se , então
Pela regra da cadeia...
Ou seja.
Show? A partir dessa função podemos responder os quatro primeiros quesitos do problema...
Veja só!
Passo 3
No item a) é pedido a velocidade em função do tempo .
Isso é justamente o que fizemos no passo 2, ou seja
No item b) é pedido a velocidade em , então substituímos em e encontramos o resultado.
No item c) temos que descobrir quando a partícula está em repolso...
Pensando fisicamente, se uma partícula está em repolso, significa que ela está parada, logo, sua velocidade é nula.
Isso acontece quando , ou seja
Ou seja, ou , ou , onde é um numero inteiro.
Já no item d) queremos saber quando a partícula está se movendo no sentido positivo, ou seja, quando
Pra essa inequação ser satisfeita, tem que ser negativo, ou seja
Multiplicamos todos os lados por para isolar no meio...
Tranquilo até aqui?
Passo 4
No item e) queremos saber qual a distancia percorrida nos primeiros segundos...
Pra isso vamos usar a função e substituímos
Bora continuar!
Passo 5
No item f) queremos ilustrar um gráfico que represente o movimento da matricula...
s
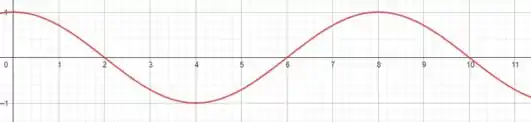
Bacana, não é?
Passo 6
No item g) queremos encontrar a função aceleração e a aceleração em .
Como vimos no passo 1.
Se , então
Pela regra da cadeia novamente...
Substituindo , temos que a aceleração nesse instante é
Estamos quase no fim!
Passo 7
No item h), o problema pediu pra plotar os gráficos de , e usando uma ferramenta gráfica...
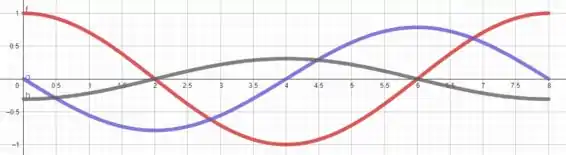
Em vermelho temos , em lilás e em preto
Show de bola?
Passo 8
Por fim, no item i) queremos determinar os intervalos em que é positivo e negativo.
Se , será positivo se o cosseno for negativo, ou seja
Multiplicamos todos os lados por para isolar no meio...
É isso! O que achou? Responde Aí!
Resposta
a)
b)
c),
d)
e)
f)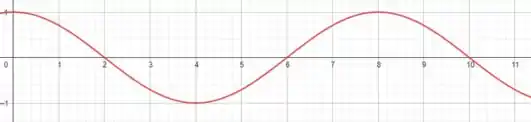 
g) ,
h)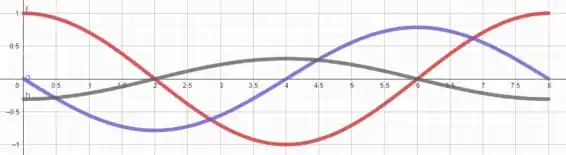 
i)