Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.5 - Ex. 64
Use o roteiro desta seção para esboçar o gráfico da curva. No passo , ache uma equação para a assíntota oblíqua.
Passo 1
Bom galera, nesse exercício iremos esboçar a curva com base no seguinte roteiro
Domínio
Intersecções com os eixos
Simetria
Assíntotas
Intervalos de crescimento e decrescimento
Valores de máximo e mínimo locais
Concavidade e ponto de inflexão
Esboço da curva
Passo 2
Domínio
Nossa função está definida para todo ponto pertencente ao conjunto dos números Reais
Intersecções com os eixos
Não há intersecção nos eixos .
Simetria
Não há simetria no gráfico.
Assíntotas
O gráfico não possui assíntotas horizontais. Isso ocorre pois quando o limite não existe
Não possui assíntotas Verticais , pois para nenhum valor temos .
Resolvendo o limite
desde que aplicando a regra de L’Hospital .
é uma assíntota oblíqua dede que enquanto
Passo 3
Intervalos de crescimento e decrescimento
Derivando a função, temos
Logo cresce em e decresce
Valores de máximo e mínimo locais
É um ponto de mínimo local e mínimo absoluto.
Não há ponto de máximo local
Concavidade e ponto de inflexão
Tirando a segunda derivada da função, temos
Para todo Logo, possui concavidade para cima para todos os valores Reais.
Não possui ponto de inflexão.
Esboço da curva
Podemos então esboçar graficamente a curva
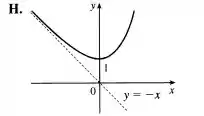
Resposta
