Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.5 - Ex. 24
Use o diagrama para mostrar que se é côncava para cima em , então
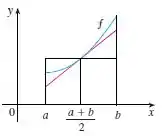
Passo 1
O enunciado pede pra a gente usar o diagrama para mostrar que se é côncava para cima em , então:
Temos também o desenho da nossa função:
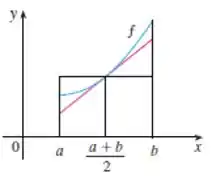
Passo 2
Bom, galerinha, o teorema do valor médio para integrais nos diz que, se uma função for contínua em , então existe um número em tal que:
A integral representa a área abaixo da curva azul e representa a área dos dois retângulos. Podemos ver no gráfico que a área abaixo da curva azul é maior que a área dos retângulos! Assim, temos que:
Passo 3
Vamos dividir por dos dois lados dessa inequação. Logo:
Como foi mostrado no passo anterior que ,
Resposta
Desenvolvimento acima.
Exercícios de Livros Relacionados
Uma barra localizada sobre o eixo dos x tem extremos x = 0 e x = 4 . Se a densidade linear é dada por ρ x = 1 x + 1 , determinar a massa e o centro de massa da barra.
O comprimento de uma barra é 2 m e a densidade linear no extremo direito é 1 kg/m. A densidade linear num ponto varia diretamente com a segunda potência da distância do ponto ao extremo esquerdo. Calc
Uma barra homogêna mede 3m de comprimento. Se o seu momento de inércia em relação a um eixo perpendicular que passa por uma de suas extremidades é 22,5k g ∙ m 2 , determinar a densidade linear da barr
Determinar a massa e o centro de massa de uma barra que está localizada sobre o eixo dos x com extremos nos pontos x = 0 e x = 1 . A densidade linear da barra é dada por ρ x = e x .
Encontrar a massa total e o centro de massa de uma barra de 5 m de comprimento, sabendo que a densidade linear num ponto é uma função do 1º grau da distância total desse ponto ao extremo direito da ba