Uma partícula move-se segunda a lei do movimento , , em que é medido em segundos e em metros
- Encontre a velocidade no instante
- Qual a velocidade depois de
- Quando a partícula está em repouso?
- Quando a partícula está se movendo no sentido positivo?
- Encontre a distância total percorrida durante os 8 primeiros segundos
- Desenhe um diagrama como na figura 2 para ilustrar o movimento da partícula
- Encontre a aceleração no instante e depois de
- Faça os gráficos das funções posição, velocidade e aceleração para
- Quando a partícula está acelerando? Quando está freando?
Passo 1
Fala aí, galerinha!! 😎

Nesse problema foi dada uma função movimento de uma partícula em relação ao tempo.
Bonitinha, né? 😁
A partir dessa função foi pedido uma serie de informações, então não vamos perder muito tempo.
A questão pede muitas coisas, então antes de cada item vamos ver como resolvemos e logo em seguida resolvemos. Combinado?
Bora lá! 😉
Passo 2
No item a) foi pedido para encontrarmos a função velocidade
Sabemos que
Portanto, pela regra do produto.
Para o nosso caso, temos
No item b) queremos obter a velocidade em , ou seja
Tranquilo até aqui? 😐
Passo 3
No item c) a partícula está em repouso quando
Logo, usando o princípio da multiplicação por zero, temos
Note que a exponencial de um número nunca será zero, logo, forma uma assíntota horizontal em
Show?
Passo 4
No item d) a partícula se move no sentido positivo quando
Para tal, devemos observar que uma função exponencial nunca retorna valores negativos, portanto
Então, devemos ter que
Legal, não é? 😎
Passo 5
No item e) sabemos que no instante . Então, calcularemos os deslocamentos nos intervalos
Então a distância total
Bora continuando...
Passo 6
Em f) esboçando o gráfico no tipo da imagem 2, ficamos com
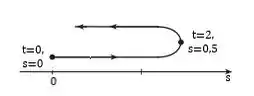
Já em g) queremos obter a função aceleração...
Sabemos que
Logo...
Interessante, né? 😉
Passo 7
No item h) fazendo os gráficos, onde

E por fim, para o item i) a partícula está acelerando quando e possuem o mesmo sinal. Logo, ela está acelerando no intervalo
A partícula está freando quando e possuem sinais opostos. Logo, ela está freando nos intervalos
É isso! O que achou? Responde Aí!
Resposta
a)
b)
c)
d)
e)
f)
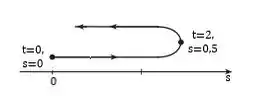
g)
h) 
i) Acelerando:
Freando: