Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 13.4 - Ex. 35
Uma partícula tem função posição . Se , onde é um vetor constante. Descreva o caminho da partícula
Passo 1
E aí, pessoal. Beleza?
A questão nos pede para dizer qual a trajetória da partícula para que seja satisfeita a relação:
Para resolvermos esta questão, precisamos relembrar um pouco sobre Geometria Analítica e tentar visualizar diferentes possibilidades. E temos que relembrar como funciona o produto vetorial.
Passo 2
A operação é um produto vetorial entre dois vetores. Das propriedades desta operação, obtemos um vetor que é perpendicular a ambos e que a base é positiva, isto é, satisfaz a regra da mão direita.
Qual é a curva em que os vetores posição e velocidade são perpendiculares em todos os pontos?
Estes critérios só serão atingidos se, e somente se, a trajetória da nossa partícula for circular, contida em um plano perpendicular ao vetor , e cujo centro está em uma reta que passa pela origem.
Vamos tentar visualizar graficamente em um exemplo abaixo:
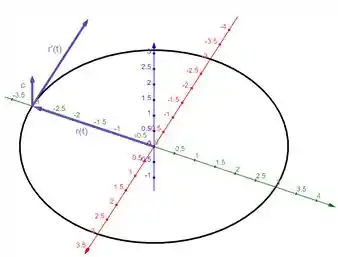
Resposta
Estes critérios só serão atingidos se, e somente se, a trajetória da nossa partícula for circular, contida em um plano perpendicular ao vetor , e cujo centro está em uma reta que passa pela origem.