Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 34
Expresse a integral dupla em termos de uma integral unidimensional com relação a . Em seguida, use a calculadora para avaliar a integral correta com quatro casas dimensionais.
Onde é a porção do disco que fica no primeiro quadrante.
Passo 1
Como a nossa região é um quarto de um disco de raio 1, o qual está localizado no primeiro quadrante, em coordenadas polares, podemos escrevê-la da seguinte forma:
Portanto, a nossa integral transforma-se em:
Passo 2
Inicialmente, vamos resolver a primeira parte da integral. Desta forma, temos:
Para resolvermos esta integral, precisamos da ajuda de softwares ou calculadoras que o resolvam. Sendo assim, temos:
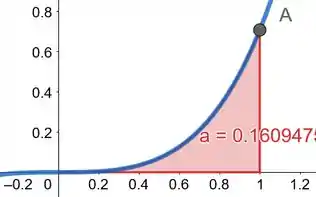
Aproximando o valor da integral para 4 casas decimais, temos:
Resposta
Exercícios de Livros Relacionados
Use coordenadas polares para determinar o volume do sólido dado.Abaixo do plano 2 x + y + z = 4 e acima do disco x 2 + y 2 ≤ 1 .
Use coordenadas polares para determinar o volume do sólido dado.Dentro da esfera x 2 + y 2 + z 2 = 16 e fora do cilindro x 2 + y 2 = 4 .
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 a ∫ - a 2 - y 2a 2 - y 22 x + y d x d y
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste para oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade nor
Use coordenadas polares para determinar o volume do sólido dado.Abaixo do paraboloide z = x 2 + y 2 e acima do disco x 2 + y 2 ≤ 25 .