Um pequeno lago contendo de galões (cerca de litros) de água não contém, inicialmente, produto químico indesejável (veja o Problema 21 da Seção 1.1). O lago recebe água contendo de um produto químico a uma taxa de e a água sai do lago à mesma taxa. Suponha que o produto químico esteja distribuído uniformemente no lago.

1. Seja a quantidade de produto químico no lago no instante . Escreva um problema de valor inicial para .
2. Resolva o problema no item (a) para . Quanto produto químico o lago terá ao final de 1 ano.
3. Ao final de 1 ano, a fonte do produto químico despejado no lago é retirada; a partir daí, o lago recebe pura, e a mistura sai à mesma taxa de antes. Escreva o problema de valor inicial que descreve essa nova situação.
4. Resolva o problema de valor inicial no item (c). Qual a quantidade de produto químico que ainda permanece no lago após mais 1 ano (2 anos após o inicio do problema)?
5. Quanto tempo vai levar para que seja igual a ?
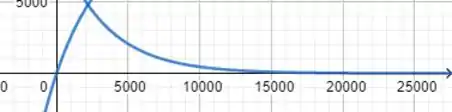
6. Faça o gráfico de em função de para até anos.

a)

Bom, vamos lá. O enunciado nos pede para montar a equação diferencial para o problema. Se olharmos no problema sugerido pelo enunciado, vamos ver algo semelhante ao nosso problema. Como inicialmente não há produto químico no lado, vamos dizer que nosso para é . Temos também que a taxa de água que entra no lago é dado por . Assim, nossa equação ficará mais ou menos da seguinte forma:

Onde nosso será a constante que irá corrigir a quantidade de produto que sai. Como dito no enunciado, a taxa que sai do lago é a mesma que entra, porém da quantidade total de água do lago. Assim, a quantidade de produto que sai é dado por . Então, nossa equação fica:

b)

Para resolvermos, vamos reescrever a equação da forma separável. Temos então que:

Integrando de ambos os lados, temos que:

Aplicando exponencial de ambos os lados, chegamos em:

Com a condição de contorno de , obtemos:

Então, nossa equação fica:

Para descobrirmos a quantidade de produto químico após um ano, primeiramente temos que transformar 1 ano em horas. Assim:

Substituindo em na equação do passo anterior, chegamos que:

.

c)

Como agora não entra mais nenhum produto químico no lago, assim o primeiro termo da nossa equação diferencial desaparece. Sendo assim, nossa equação agora se torna:

E nosso agora vai ser o valor que se encontra no final de um ano, como o achado no passo anterior. Assim, .

d)

Como no item (c), vamos tornar separável nossa equação.

Integrando de ambos os lados, temos:

Aplicando exponencial, temos:

Com a condição de contorno, chegamos em:

Assim:

Após mais um ano, temos que nosso será . Substituindo na equação, vamos ter que:

e)

Agora queremos o tempo para chegar em . Assim, temos que, aplicando o logaritmo natural em ambos os lados, ficamos com:

Para , temos:

f)