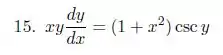Exercícios de EDO Separável - Lista de Exercícios Resolvida
Questão 1
Resolva a equação diferencial dada por separação de variável descrita abaixo:
Ver solução completaQuestão 4
Considere a equação diferencial :
Ache a solução geral explícita desta equação diferencial.
Ver solução completaQuestão 5
Considere a equação diferencial
Ache a solução geral.
Resolva o problema de valor inicial com a condição inicial .
Ver solução completaQuestão 7
Indique qual das afirmativas abaixo é verdadeira.
(a) a equação não admite soluções constantes.
(b) toda solução da equação é uma função crescente.
(c) todas as outras afirmativas são falsas.
(d) a equação é linear
(e) a equação é separável.
Ver solução completaQuestão 8
Resolva o problema de valor inicial abaixo, isto é, encontre a função ou as funções que satisfaz(em) a equação diferencial e as condições iniciais dadas.
Ver solução completaQuestão 9
Considere a seguinte equação diferencial:
Encontre a solução da equação diferencial com condição inicial .
Ver solução completaQuestão 12
Considere a equação diferencial :
Ache a solução geral explícita desta equação diferencial.
Determine a solução parcial que passa pelo ponto
O problema de valor inicial e tem solução?
Ver solução completaQuestão 13
- Mostre que a equação
É separável
- Resolva a mesma
- Ache a solução tal que
Ver solução completaÉ separável
Questão 14
Resolva os problemas de valor inicial abaixo, isto é, encontre a função que satisfaz a equação diferencial e as condições iniciais dadas.
(b)
Ver solução completaQuestão 16
Resolva os problemas de valor inicial abaixo, isto é, encontre a função que satisfaz a equação diferencial e as condições iniciais dadas.
(a)
Ver solução completaQuestão 17
Sabendo que após ser coado o café está a e, um minuto depois, passa para , em uma cozinha a . Determine a temperatura do café em função do tempo e o tempo que levará para o café chegar a .
Ver solução completaQuestão 18
Questão 1: Resolva as seguintes equações diferenciais e problemas de valor inicial, conforme seja o caso:
Ver solução completaQuestão 20
Qual a única resposta correta como solução da ED : ?
( )
( )
( )
( )
( )
Ver solução completaQuestão 21
Nos exercícios a verifique que a equação é de variáveis separáveis e resolva-a.
Ver solução completa
Questão 31
Marque a alternativa que contenha a solução geral da equação diferencial separável
Questão 35
Nos exercícios a verifique que a equação é de variáveis separáveis e resolva-a.
Ver solução completa
Questão 36
Considere o problema de valor inicial relativo à queda livre a partir do repouso, considerando a resistência do ar como uma força oposta ao movimento e proporcional à velocidade. A constante gravitacional é aproximadamente constante próxima à superfície da Terra.
Determine a solução do problema de valor inicial.
Determine em quanto tempo o corpo atinge o solo, se começa a de altura.
Neste item, considere, e obtenha um resultado aproximado.
Dica: Utilize a lei de Newton peso + resistência do ar .
Dica: Oriente o eixo verticalmente para baixo, colocando a origem na posição inicial.
Ver solução completaQuestão 37
Considere a seguinte equação diferencial:
Encontre solução da equação diferencial com condição inicial .
Ver solução completaQuestão 38
Considere a seguinte equação diferencial:
Encontre a solução da equação diferencial com condição inicial .
Ver solução completaQuestão 39
Use a substituição (redução de ordem), obtenha a solução para a seguinte EDO de ordem , e responda se a solução obtida é implícita ou explícita:
Ver solução completaQuestão 40
Considere a equação diferencial
Ache a solução geral.
Resolva o problema de valor inicial com a condição inicial .
Ver solução completaQuestão 41
O número de soluções constantes da equação diferencial
É:
- Infinito
- Nenhuma das demais alternativas
Questão 43
Seja a solução do problema de valor inicial
Quanto vale ?
- Nenhuma das demais respostas
Questão 44
Questão 3: Dada a equação diferencial :
- Determine em que pontos do plano as condições do Teorema da existência e unicidade são válidas.
- Resolva o problema de valor inicial
- Determine o maior intervalo em que a solução do item pode estar definida.
Questão 45
Marque a alternativa que indica a solução da eq. diferencial de variáveis separáveis.
( )
( )
( )
( )
( )
Ver solução completaQuestão 47
- Encontre a solução de forma explicita do problema de valor inicial
- Mostre que a solução é única. Usando o conhecimento da Matéria, responda:
Para que valores de , podemos garantir que a solução existe e é única, substituindo a condição inicial por ? (Não esqueça de justificar, com a teoria vista).
Ver solução completaQuestão 48
Considere uma população de cardume de peixes, avaliada em centenas de milhares de peixes em centenas de dias. Os peixes são pescados com certa frequência e dada suas taxas de reprodução, as populações evoluem de acordo com
Sabendo que ( 260 mil peixes), calcule quantos dias teremos até a extinção dos peixes neste lago, ou seja, tal que . (Aproximado a uma casa decimal)
Escolha uma:
dias
dias
dias
dias
dias
Ver solução completaQuestão 52
Resolve as seguintes equações diferenciais. No caso da letra a), resolve o problema de valor inicial associado.
Questão 53
A equação separável
Admite apenas a solução trivial como solução constante.
Verdadeiro ou falso?
Ver solução completaQuestão 54
A equação separável
Admite solução constante igual a .
Escolha uma opção:
Verdadeiro
Falso
Ver solução completaQuestão 55
A equação separável
Admite duas soluções constantes iguais a e . Escolha uma opção:
Verdadeiro
Falso
Ver solução completaQuestão 56
Marque a alternativa que contenha a solução geral da equação diferencial separável
Questão 57
Marque a alternativa que contenha a solução geral da equação diferencial separável
Questão 58
Considere a seguinte equação diferencial:
- Verifique se é uma solução para a equação diferencial.
- Encontre a solução da equação diferencial com condição inicial .
Questão 60
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 61
Nos problemas de (a) até (l), encontre a solução geral da equação diferencial dada. Dê o maior intervalo I sobre o qual a solução geral está definida.
Ver solução completaQuestão 66
4. Coloca-se uma barra de metal à temperatura de em um quarto com temperatura constante de . Se, após 20 min, a temperatura da barra é de , determine:
a) O tempo necessário para que a barra chegue à temperatura de .
Ver solução completaQuestão 74
Responda falso ou verdadeira justificando a sua resposta, ou seja, prove se for verdadeiro ou dê um contra exemplo se for falso:
Toda equação diferencial separável é exata.
Ver solução completaQuestão 75
Seja a equação diferencial:
- Determine o comportamento da solução desta equação quando , dependendo do valor inicial
- Encontre a solução Geral da equação diferencial
Questão 76
Considere a seguinte equação diferencial:
Encontre a solução da equação diferencial com condição inicial .
Ver solução completaQuestão 77
Resolva a seguinte equação diferencial ou problema de valor inicial conforme caso abaixo:
Ver solução completaQuestão 78
Seja a equação diferencial ordinária
Obtenha a solução geral da EDO acima.
Ver solução completaQuestão 79
Resolva a equação diferencial , , mediante a mudança de variáveis (ou seja, ); onde deve ser escolhido convenientemente de modo a obter uma EDO (em termos de ) separável.
Ver solução completaQuestão 80
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 81
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 82
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 83
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 84
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 85
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 86
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 87
Considere a equação diferencial:
- Obtenha a solução geral.
- Considere a condição inicial e determine a solução particular para esta condição inicial.
- Existe alguma soluçaõ de equilíbrio? Determine todas que houver. Se não houver, explique o por quê.
Questão 90
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 94
Questão 1: Resolva as seguintes equações diferenciais ou problemas de valor inicial, conforme seja o caso.
Ver solução completaQuestão 95
Se é a solução do problema de valor inicial
Então é errado afirmar que
- é limitada
- é decrescente
- para todo
Questão 97
Considere a equação diferencial
- Obtenha a solução geral explícita da equação diferencial acima.
- Determine a solução da equação diferencial acima que satisfaz a condição inicial
Questão 100
Resolva a equação diferencial dada abaixo por separação de variáveis.
( )
( )
( )
( )
( )
Ver solução completaQuestão 102
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 103
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 104
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 105
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 106
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 107
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 108
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 109
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 110
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 111
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 112
Nos problemas de (a) até (d), encontre uma solução para o problema de valor inicial dado
Ver solução completaQuestão 113
Nos problemas de (a) até (d), encontre uma solução para o problema de valor inicial dado
Ver solução completaQuestão 114
Nos problemas de (a) até (d), encontre uma solução para o problema de valor inicial dado
Ver solução completaQuestão 115
Nos problemas de (a) até (d), encontre uma solução para o problema de valor inicial dado
Ver solução completaQuestão 116
Frequentemente, uma pequena mudança na condição inicial ou na equação diferencial, geram uma mudança radical na solução da equação diferencial. Nos problemas de (a) até (d), encontre uma solução explícita para o problema de valor inicial dado, trace um gráfico da solução encontrada e compare cada curva da solução em uma vizinhança de (0;1).
Ver solução completaQuestão 117
Frequentemente, uma pequena mudança na condição inicial ou na equação diferencial, geram uma mudança radical na solução da equação diferencial. Nos problemas de (a) até (d), encontre uma solução explícita para o problema de valor inicial dado, trace um gráfico da solução encontrada e compare cada curva da solução em uma vizinhança de (0;1).
Ver solução completaQuestão 118
Nos problemas de (a) até (k), resolva a equação diferencial dada usando o método de separação de variáveis
Ver solução completaQuestão 119
Sabendo que ao realizarmos a mudança de variável , onde é uma solução da EDO
obtemos a seguinte EDO de Bernoulli
Use esse resultado para resolver a seguinte EDO
com
Ver solução completaQuestão 120
Frequentemente, uma pequena mudança na condição inicial ou na equação diferencial, geram uma mudança radical na solução da equação diferencial. Nos problemas de (a) até (d), encontre uma solução explícita para o problema de valor inicial dado, trace um gráfico da solução encontrada e compare cada curva da solução em uma vizinhança de (0;1).
Ver solução completaQuestão 121
Frequentemente, uma pequena mudança na condição inicial ou na equação diferencial, geram uma mudança radical na solução da equação diferencial. Nos problemas de (a) até (d), encontre uma solução explícita para o problema de valor inicial dado, trace um gráfico da solução encontrada e compare cada curva da solução em uma vizinhança de (0;1).
Ver solução completaQuestão 122
Resolva as seguintes equações diferenciais, pelo método de separação de variáveis
Ver solução completaQuestão 123
Resolva as seguintes equações diferenciais, e problemas de valor inicial.
Ver solução completa