Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.3 - Ex. 17

Uma piscina tem 2 0   m de largura, 4 0   m   de comprimento e seu fundo é um plano inclinado. O extremo mais raso tem uma profundidade de   3   m e o extremo mais fundo, 9   m . Se a piscina estiver cheia de água, calcule a força hidrostática (a) na extremidade mais rasa, (b) na extremidade mais funda, (c) em um dos lados e (d) no fundo da piscina.

Passo 1

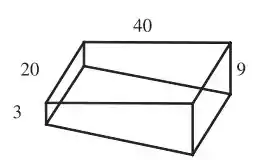
  1. O esboço da piscina é o seguinte:

    2. A área na extremidade mais rasa é 20 ∆ x , e a pressão nessa área é δ x i . Assim, a força nessa área é

    F = ∫ 0 3 δ x   20 d x = 20 δ 1 2 x 2 0 3 = 20 δ 9 2 = 9 0 δ = 90 62.5 =

    5625 l b ≈ 5.63 × 10 3 l b

    Passo 2

  2. Seguimos o mesmo caminho do exercício anterior, mas agora x varia entre 0 e 9 , que representa a profundidade dessa área:

    3. F = ∫ 0 9 δ x   20 d x = 20 δ 1 2 x 2 0 9 = 20 δ 81 2 = 81 0 δ = 81 0 62.5 =

    50,6 25 l b ≈ 5.06 × 10 4 l b

    Passo 3

  3. Para o comprimento de 3   m , a gente tem o lado constante em 40   m . Para 3 < x ≤ 9 , nós podemos usar semelhança de triângulos para achar o valor de um a hipotético, assim:

    4. a 40 = 9 - x 6 → a = 40 9 - x 6

    Agora bora calcular a força:

    F = ∫ 0 3 δ x   4 0 d x + ∫ 3 9 δ x   40 9 - x 6 d x = 4 0 δ 1 2 x 2 0 3 + 20 δ ∫ 3 9 9 x - x 2 d x =

    18 0 δ + 20 3 δ 9 2 x 2 - 1 3 x 3 3 9 = 180 δ + 20 3 δ 729 2 - 243 - 81 2 - 9 = 18 0 δ + 60 0 δ

    = 7 80 δ = 78 0 62.5 = 48,740 l b ≈ 4.88 × 10 4 l b

    Passo 4

  4. A gente pode pensar na seguinte figura:

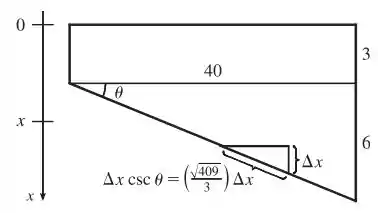
Para qualquer triângulo com hipotenusa na parte inferior, como vemos na figura, teremos

sin ⁡ θ = ∆ x h i p o t e n u s a → h i p o t e n u s a = ∆ x csc ⁡ θ = ∆ x 40 2 + 6 2 6 = 409 3 ∆ x

Então, a força obtida é

F = ∫ 3 9 δ x   20 409 3 d x = 1 3 20 409 δ 1 2 x 2 3 9 = 1 3 10 409 δ 81 - 9 ≈ 303,356 l b

≈ 3.03 × 10 5 l b  

Resposta

  1. 5.63 × 10 3 l b
  2. 5.06 × 10 4 l b
  3. 4.88 × 10 4 l b
  4. 3.03 × 10 5 l b
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
Um aquário de 5 pés de comprimento, 2 pés de largura e 3 pés de profundidade está cheio de água. Descubra (a) a pressão hidrostática no fundo do aquário, (b) a força hidrostática no fundo e (c) a forç
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Ent