Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 8.3 - Ex. 9
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Então expresse a força como uma integral e calcule-a
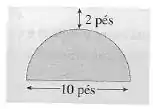
Passo 1
Podemos ilustrar a situação da seguinte forma
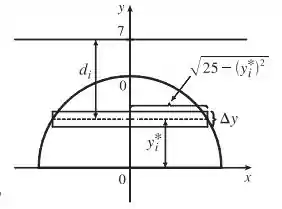
Temos que o comprimento da linha pontilhada mostrada na figura é dada por , então, a área do retângulo mostrado na figura é
A pressão é dada por . Então podemos escrever a força como
Temos que
Então, podemos escrever como uma integral
Resposta
Exercícios de Livros Relacionados
Uma barragem vertical tem um portão semicircular, como mostrado na figura. Calcule a força hidrostática contra o portão.
Uma placa vertical com uma forma irregular é imersa na água. A tabela mostra as medidas de suas larguras de acordo com a profundidade. Usa a Regra de Simpson para estimar a força da água contra a plac
Uma vala é preenchida com um líquido de densidade 840k g / m 3 . As extremidades da vala são triângulos equiláteros com lados de 8m de comprimento e o vértice no fundo. Calcule a força hidrostática em
Um tanque grande é projetado com as extremidades no formato da região entre as curvas y = 1 2 x 2 e y = 12 , medidas em pés. Calcule a força hidrostática em uma extremidade do tanque se ele estiver ch
Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada nas figuras a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. E