Uma placa vertical é imersa (ou parcialmente imersa) na água e tem a forma indicada na figura a seguir. Explique como aproximar a força hidrostática em um lado da placa usando uma soma de Riemann. Então expresse a força como uma integral e calcule-a

Podemos ilustrar a situação da seguinte forma

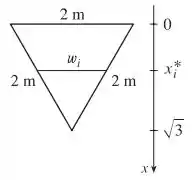
Então, sabemos que a pressão varia em função da altura onde um ponto está dentro do recipiente, ou seja, pontos há mesma altura, possuem a mesma força sendo exercida sobre a parede, então precisamos escrever a força como uma soma de Riemann (note que a ). A base do triângulo mostrado na figura é dada por, então, e podemos escrever a área como (fizemos por semelhança de triângulos)

Então a força

Temos que

Então, podemos escrever como uma integral