Os pneus de automóveis precisam ser inflados corretamente porque uma pressão interna inadequada pode causar um desgaste prematuro. Os dados na tabela mostram a vida útil do pneu (em milhares de quilômetros) para um certo tipo de pneu em pressões (em kPa)

1. Use uma calculadora gráfica ou computador para modelar a vida do pneu como uma função quadrática da pressão.
2. Use o modelo para estimar quando e quando . Qual o significado da derivada? Quais são suas unidades? Qual é o significado dos sinais das derivadas?

A primeira coisa que precisamos fazer é modelar a função quadrática que relaciona a arelaciona a vida útil de um pneu com sua pressão interna::

Aqui vamos usar o excel, então vamos criar uma coluna com os dados de , esse vai ser nosso eixo e a outra coluna com os dados de vai ser nosso eixo .

Após isso a gente vai plotar o gráfico de dispersão e selecionar a opção de regressão quadrática, ficamos então com:

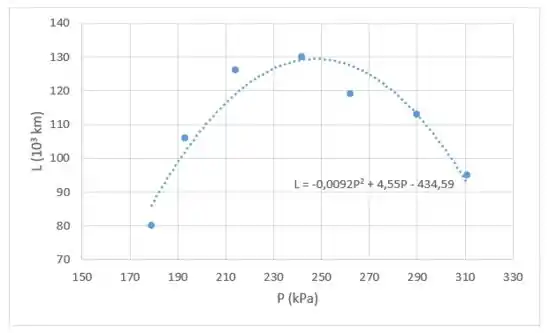
Temos então que o ajuste quadrático será:

Agora vamos derivar e encontrarmos o valor da derivada para e :

Sua respectiva derivada será determinada pela regra da potência, em que a derivada de elevado ao expoente , será igual ao expoente vezes elevado ao expoente menos 1, como o exemplo abaixo.

Calculando:

Como a unidade de é quando derivarmos em relação a que está em . Podemos simplificar como:

Usando a equação de e substituindo por e , teremos que

Para :

Fazendo as contas:

Para :

Fazendo as contas:

Pra finalizar, vamos entender melhor o significado da derivada. A derivada representa a variação da vida útil do pneu com relação ao tempo. Assim, se a derivada é positiva a vida útil do pneu aumenta e se for negativa ela diminui.