Uma partícula move-se segundo a lei do movimento , , onde é medido em segundos e , em pés.

(a) Encontre a velocidade no instante .

(b) Qual a velocidade depois de 3 s?

(c) Quando a partícula está em repouso?

(d) Quando a partícula está se movendo no sentido positivo?

(e) Encontre a distância total percorrida durante os 8 primeiros segundos.

(f) Desenhe um diagrama como na Figura 2 para ilustrar o movimento da partícula.

Para saber quando a partícula esta em repouso, é quando , certo? Portanto,

Ou

Essa é bem simples!

Para saber quando a partícula esta se movendo no sentido positivo, é quando , certo? Portanto, se e , os valores de devem estar entre

Ou

A distância total percorrida durante os 8 primeiros segundos é dada pela diferença entre os valores até chegar em , vamos lá:

Somando esses valores temos que a distancia total é .

O diagrama que representa esse movimento da partícula é:

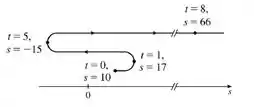
Prontinho!!