Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.4 (exercícios de compreensão) - Ex. 3
Se é um ponto no gráfico de uma função ímpar invertível, então _______ e _______ são pontos no gráfico de
Passo 1
Show galera, saca só. Pra lembrar, toda função ímpar é uma função que, em matematiquês, tem valendo:
E em grafiquês é como se a função fosse espelhada em relação ao eixo e depois em relação eixo . A ordem contrária também daria no mesmo:
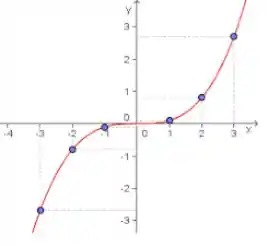
Beleza gente, então se sabemos que é um ponto do gráfico e sabemos que , temos que:
E portanto, o ponto também será um ponto desse gráfico! Show de bola!
Passo 2
Aaaa mais perai cara, a questão nem ta falando de e sim de . Calma galerinha, olha só, sabemos dois pontos que fazem parte da função , né não?
E sabemos que a função é invertível! Oras, quando a gente inverte uma função, a gente acaba trocando de lugar em todos os seus pontos! Portanto, trocando nos pontos acima:
Taí! Dois pontos que temos certeza que são pontos do gráfico de ! Feshow!
Resposta
Os pontos e fazem parte do gráfico de de