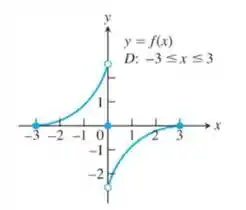
Em que pontos do domínio a função parece ser
- derivável?
- contínua, mas não derivável?
- nem contínua, nem derivável?
Passo 1
Primeiro, podemos notar que a função é definida por partes, logo, pode não ser derivável em todos os pontos.
Passo 2
Respondendo o item (a)
Para e para
Podemos perceber que a função é continua e derivável.
Passo 3
Respondendo o item (b)
Além dos pontos citados no item (a), não outros pontos onde a função é contínua.
Passo 4
Respondendo o item (c)
Podemos notar que para os limites laterais não são iguais e não coincidem com o valor de . Logo, a função não é continua e não parece ser derivável.
Resposta
Ei, a resposta está no passo a passo :)