Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 7.Exercícios de Revisão - Ex. 27

Nos problemas 25-28, (a) expresse f em termos de função degrau unitário, (b) calcule L f t e (c) calcule L e t f t

Passo 1

E aíí cara, vamos lá!

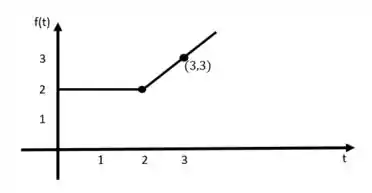
Temos esse gráfico aqui de f ( t ) :

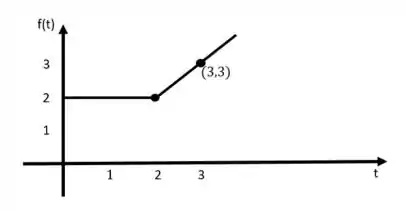
(a) E pra começar, vamos escrever essa função em termos do degrau unitário u , beleza?

Vamos ver: nossa função vale 2 entre 0 e 2 e vale t para t ≥ 2 . Então podemos escrever assim:

f t = 2 + t - 2 u ( t - 2 )

Agora vamos pros próximos itens!!

Passo 2

(b) Vamos agora calcular L f t :

L 2 + t - 2 u ( t - 2 )

Usando as técnicas que vimos até o momento, temos;

L 2 + t - 2 u ( t - 2 ) = 2 s + 1 s ² e - 2 s

Fechouuu? Agora só mais um item, boraa

Passo 3

(c) Agora temos que calcular L e t f t

L e t f t = L 2 e t + t - 2 e t u ( t - 2 )

Bom gente, o e t multiplicando vai causar a translação em uma amostra no domínio s , então:

L 2 e t + t - 2 e t u ( t - 2 ) = 2 s - 1 + 1 ( s - 1 ) ² e - 2 ( s - 1 )

Fechouuuuu

Resposta

a )   f t = 2 + t - 2 u ( t - 2 )

b )   L 2 + t - 2 u ( t - 2 ) = 2 s + 1 s ² e - 2 s

c )   L 2 e t + t - 2 e t u ( t - 2 ) = 2 s - 1 + 1 ( s - 1 ) ² e - 2 ( s - 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas 3-24, preencha as lacunas ou responda verdadeiro/falso.Se L f t = F ( s ) e k0 , então L e a t - k f t - k u t - k = _ _ _ _ _ _ _ _
Nos problemas 3-24, preencha as lacunas ou responda verdadeiro/falso. L - 1 20 s 6
Nos problemas 3-24, preencha as lacunas ou responda verdadeiro/falso. L e - 3 t s e n ( 2 t )
Nos problemas 3-24, preencha as lacunas ou responda verdadeiro/falso. L - 1 1 ( s - 5 ) ³ ³
Nos problemas 3-24, preencha as lacunas ou responda verdadeiro/falso. 1 * 1 = _ _ _ _ _