Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.5 - Ex. 9
Os problemas de 8 a 13 envolvem equações da forma Em cada problema, esboce o gráfico de em função de , determine os pontos críticos (de equilíbrio) e classifique-os como assintoticamente estável, instável ou semiestável (veja o Problema 7). Desenhe a reta de fase e esboce diversos gráficos de soluções no plano
Passo 1
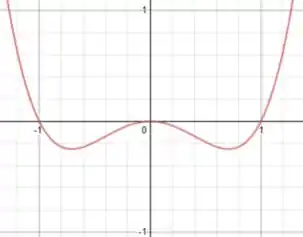
9- Nessa questão vamos esboçar o gráfico da função:
Com condição inicial no intervalo . O gráfico é
Passo 2
O esboço das diversas soluções é:
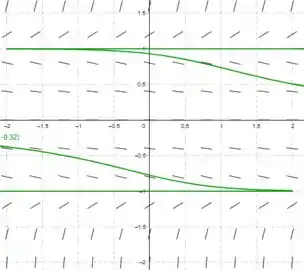
Teremos três pontos de equilíbrio um em , outro em e mais um em , como podemos ver pelo tracejado, as soluções em torno de se aproximam da solução então é um ponto de equilíbrio estável, em torno de elas se aproximam para mas se afastam para o que indica equilíbrio semiestável. E para , as soluções divergem tanto por cima, quanto por baixo, , se afastando do equilíbrio, então ele é instável.
Passo 3
Com isso, a gente pode escrever a reta de fases de acordo com a maneira que as soluções se afastam ou se aproximam dos pontos de equilíbrio:
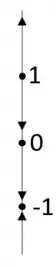
Resposta
Ei, a resposta está no passo a passo :)