Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.5 - Ex. 26

Ponto de Bifurcação. Para uma equação da forma,

d y / d t = f ( a , y ) ,     ( i )

Em que a é um parâmetro real, os pontos críticos (soluções de equilíbrio) dependem, em geral, do valor de a . Quando a aumenta ou diminui constantemente, acontece, muitas vezes, que, para determinado valor de a , chamado de ponto de bifurcação, os pontos críticos se juntam, ou se separam, e soluções de equilíbrio podem ser perdidadas ou podem aparecer. Pontos de bifurcação são de grande interesse em muitas aplicações porque, perto deles, a natureza das soluções da equação diferencial subjacente muda bruscamente. Por exemplo, em mecânica dos fluidos, um fluxo suave (laminar) pode se dispersar e se tornar turbulento. Ou uma coluna com carga axial pode empenar, subitamente, e exibir um grande deslocamento lateral. Ou, quando a quantidade de um dos produtos químicos em uma mistura aumenta, podem aparecer, subitamente, padrões de diversas cores em ondas espirais em um fluido originalmente quieto. Os problemas de 25 a 27 descrevem três tipos de bifurcação que podem ocorrer em equações simples da forma (i).

26. Considere a equação

d y d t = a y - y 3 = y a - y 2 ,   ( i i i )

(a) Considere, novamente, os casos a < 0 ,   a = 0 e a > 0 . Em cada caso, encontre os pontos críticos, desenhe a reta de fase e determine se cada ponto crítico é assintoticamente estável, semiestável ou instável.

(b) Em cada caso, esboce diversas soluções da Eq.(iii) no plano t y .

(c)Desenhe o diagrama de bifurcação para a Eq.(iii), ou seja, faça o gráfico da localização dos pontos críticos em função de a . Para a Eq.(iii), o ponto de bifurcação em a = 0 é chamado de bifurcação tridente; seu diagrama pode sugerir por que esse nome é apropriado.

Passo 1

Aqui vamos seguir o mesmo raciocínio do exercício anterior.

Passo 2

(a) Para sabermos quais são os pontos de equilíbrio de uma função, basta tomarmos quando sua derivada é nula, neste casa

d y d t = a y - y 3 = y a - y 2 = 0

Ou seja

y = ± a ou y = 0

Assim temos que, para a > 0 , temos y 1 = a e y 2 = - a . Para a = 0 , temos y = 0 . E para a < 0 , não temos raízes reais, e como estamos trabalhando no conjunto dos reais, dizemos que não a pontos de há pontos de equilíbrio para essa condição.

Passo 3

(b) Tomando valores a = - 1 , a = 0 e a = - 1

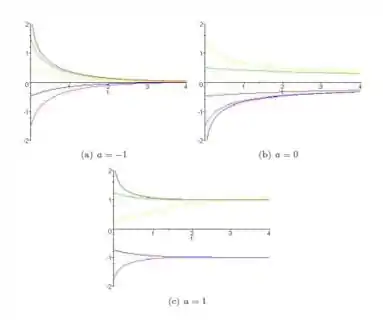
Passo 4

(c) O nosso gráfico de localização é dado pela figura abaixo

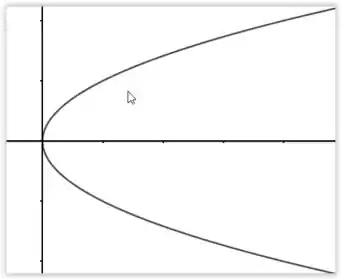
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre, por meio de diferenciação, que a função C t = a ⋅ ln ⁡ y t - b ⋅ y t - d ⋅ x t + c ⋅ ln ⁡ x t é constante quando x ( t ) e y ( t ) são positivos e satisfazem as equações presa-predador. Enquan
Aproximação do equilíbrio por duas trajetórias. Mostre que as duas trajetórias que conduzem a ( m / n ,a / b ) mostradas na Figura 9.31 são únicas por meio dos passos seguintes.A partir do sistema 1 a
Difusão de informação. Os sociólogos reconhecem um fenômeno chamado difusão social, que é a propagação de uma informação, inovação tecnológica ou modismo cultural entre a população. Os membros da popu
As equações diferenciais autônomas representam modelos de crescimento populacional. Use a análise da reta de fase para esboçar curvas integrais P ( t ) , selecionando diferentes valores iniciais P ( 0
Variação catastrófica no crescimento logístico. Suponha que uma população saudável de algumas espécies cresça em um ambiente limitado e que a população atual P 0 esteja bastante próxima da capacidade