Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.Revisão - Ex. 77
Prove que se x dor qualquer número real, .
Passo 1
Neste passo podemos analisar cada termo na desigualdade separadamente para comprovar que para todo valor real de x o seu módulo será menor que o termo .
Para provar essa afirmativa nós podemos desenhar os gráficos para as duas funções dadas:
Sendo assim:
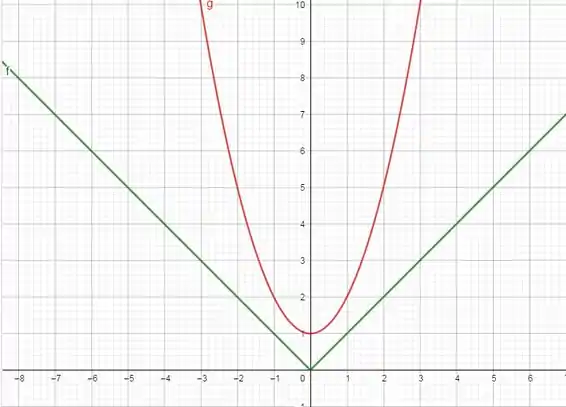
Pelo gráfico nós podemos observar que para todos os valores reais de :
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Uma xícara com café quente está sobre a mesa. Você despeja leite frio nela e espera por uma hora. Esboce um gráfico aproximado da temperatura do café como uma função do tempo
Conforme vimos no Exemplo 3, a equação x 2 + y 2 = 25 não define y como uma função de x . Cada gráfico nestes exercícios é uma porção do círculo x 2 + y 2 = 25 . Em cada caso, determine se o gráfico d
Conforme vimos no Exemplo 3, a equação x 2 + y 2 = 25 não define y como uma função de x . Cada gráfico nestes exercícios é uma porção do círculo x 2 + y 2 = 25 . Em cada caso, determine se o gráfico d
Conforme vimos no Exemplo 3, a equação x 2 + y 2 = 25 não define y como uma função de x . Cada gráfico nestes exercícios é uma porção do círculo x 2 + y 2 = 25 . Em cada caso, determine se o gráfico d
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta19. Uma curva que cruza o eixo x em dois pontos distintos não pode ser o gráfico de uma função.