Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.4 - Ex. 12
Nos exercícios de 5 a 12, remova da equação dada o termo por uma rotação de eixos. Faça um esboço do gráfico e mostre os dois conjuntos de eixos.
Passo 1
Para efetuar a rotação, vamos usar os seguintes fatos:
- Se for a representação de um ponto em relação a um conjunto de eixos e for a representação de após a rotação dos eixos de um ângulo , então
- Se , a equação pode ser transformada na equação onde e não são ambos nulos, por uma rotação de eixos de ângulo para o qual .
Nós temos a equação e vamos remover o termo , então vamos utilizar a fórmula de (2).
Passo 2
Agora para usar o fato 1 precisamos achar e . Usaremos as relações:
Queremos , daí, como e , então pertencerá ao segundo quadrante e com , podemos montar o seguinte triângulo e achar as relações.
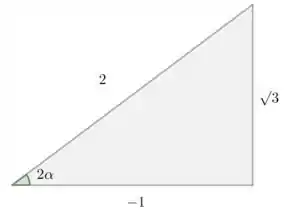
Se no triângulo imaginário acima a gente utilizasse , também faríamos uma rotação correta, porém iria pertencer ao segundo quadrante e basicamente seria a rotação que vamos fazer mais um ângulo de .
Com , temos:
Passo 3
Agora vamos usar os dados acima para trocar as coordenadas com a fórmula:
Substituindo na nossa equação, ficamos com:
Simplificando essa expressão, nós obtemos a equação:
Que é a equação de uma hipérbole com centro na origem e sem o termo .
Passo 4
Como , então o ângulo de rotação foi . Sendo assim, segue o esboço da hipérbole com o eixo OXY e os eixos rotacionados .
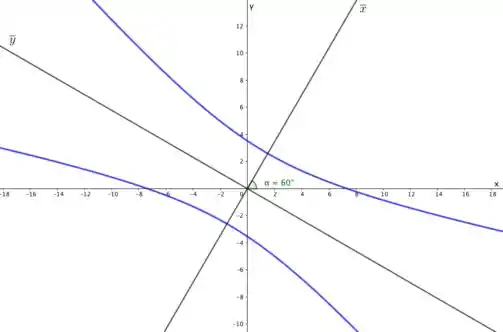
Resposta
Ei, a resposta está no passo a passo :)