Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 11
Qualquer secção de um espelho parabólico feita por um plano que passa pelo eixo do espelho é um segmento de parábola. A altura do segmento é 12 cm e o comprimento da base é 18 cm. Uma secção do espelho feita por um plano perpendicular ao eixo é uma circunferência. Ache a circunferência da secção plana circular se o plano perpendicular ao eixo estiver a 3 cm do vértice.
Passo 1
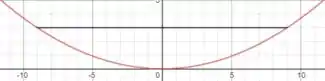
Bom, vamos supor q o espelho está com a sua concavidade virada para cima, então ao passarmos um plano vertical pelo eixo, cortaremos ele e obteremos uma parábola nesse corte. E se cortarmos horizontalmente, obteremos uma circunferência. Com isso, o enunciado nos dá algumas medidas dessa parábola. Então vamos usar a equação da parábola onde seu eixo é o eixo y:
Como e , pois colocamos o vértice na origem:
Passo 2
O enunciado nos deu a altura, 12cm, então temos uma coordenada y, e o outro dado é o comprimento da base, 18cm, então temos uma coordenada x. Substituindo na equação da parábola:
Nossa equação da parábola então é:
Passo 3
E agora, podemos calcular a circunferência do corte horizontal, vamos substituir os 3 cm dados no enunciado em y, que será a altura onde o plano horizontal irá passar para formar a circunferência:
E então a distância entre os dois valores de x na parábola pode ser calculada medindo a diferença, assim obtemos um segmento de reta que vai de um valor a outro de x:
Esse será o diâmetro da nossa circunferência, e agora pela equação do comprimento da circunferência: