Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.2 - Ex. 26
Quando ratos de laboratórios são expostos a fibras de amianto, alguns deles desenvolvem tumores no pulmão. A tabela lista os resultados de diversas experiências de diferentes cientistas.
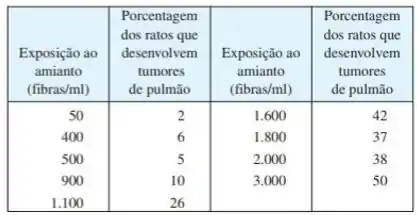
(a) Encontre uma reta de regressão para os dados;
(b) Faça um diagrama de dispersão e trace a reta de regressão. A reta de regressão parece um modelo adequado para os dados?
(c) O que a interseção com o eixo da reta de regressão representa?
Passo 1
Eaeee, belezinha?? Bom... a questão nos dá a seguinte tabela que relaciona a exposição de ratos de laboratório ao amianto (dados em fibras/ml) e a porcentagem desses animais que desenvolvem tumores de pulmão :
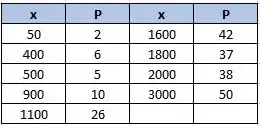
Queremos encontrar uma reta de regressão para esses dados. Ou seja, com o auxílio de uma calculadora gráfica, devemos aplicar esses dados e analisar a equação resultante.
Depois temos que traçar essa reta no gráfico e comparar com os pontos para vermos se podemos adotar a equação para outros valores da pesquisa realizada.
E aí? Bora lá?? 😉
Passo 2
Bom... aplicando os valores da tabela em um software matemático, encontramos a seguinte equação da reta:
Plotando essa reta e aplicando os pontos no gráfico, temos:
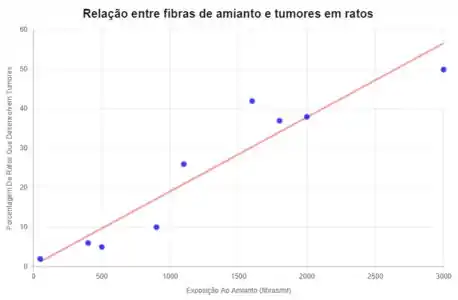
Note que a reta de regressão gerada parece um modelo adequado para os dados.
Passo 3
A interseção da linha de regressão com o eixo representa a porcentagem de ratos com tumores quando não há exposição de amianto.
Ou seja, perceba que o gráfico irá cruzar o eixo em , que é justamente o que se espera (que não tenham ratos com tumores porque não foram expostos ao amianto!!).
Entendeu direitinho?? Responde aee 😉
Resposta
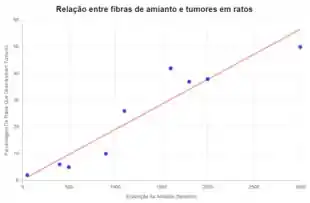
- A interseção da linha de regressão com o eixo representa a porcentagem de ratos com tumores quando não há exposição de amianto.