Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 49b
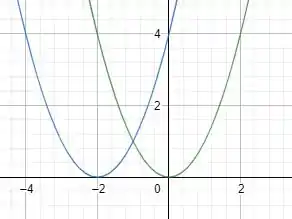
Identifique algebricamente as transformações realizadas na parábola “mãe” , para obter as seguintes funções quadráticas. A seguir trace o gráfico e compare os resultados.
b)
Passo 1
Então galera, a nossa função base é a função , então para podermos realizar essa comparação teremos que reescrever a função que nos foi dada de outra maneira, tudo bem? Uma coisa interessante de se fazer aqui é escrever esse polinômio como um produto notável, saca só:
Agora que reescrevemos a nossa função podemos analisar as transformações e o gráfico!
Passo 2
Quando temos uma função que apresenta uma soma ou subtração diretamente na variável, ou seja, uma função desse tipo aqui:
Isso implica que o gráfico da função vai ser deslocado ou transladado horizontalmente, tudo bem? Se for uma soma o gráfico vai ser deslocado para a esquerda. Se for uma subtração o gráfico vai ser deslocado para a direita. No nosso caso tem uma soma de unidades, então o gráfico vai ser deslocado para a esquerda em unidades.
Como essa é a única transformação, então já podemos plotar o gráfico, se liga:
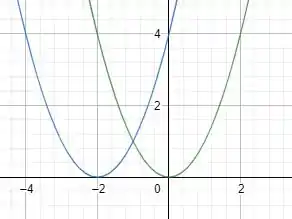
No qual a função em verde é a função e a função em azul é a função . E esse é o nosso resultado, pessoal! 😊
Resposta
Transformação:
Deslocado para a esquerda em unidades.
