Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.2 - Ex. 27
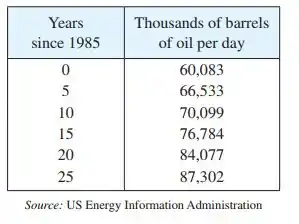
A tabela mostra a média mundial de consumo de petróleo desde 1985 até 2010, medida em milhares de barris por dia.
a) Faça um gráfico com os pontos da tabela e diga se um modelo linear é apropriado.
b) Faça um gráfico com a linha de regressão.
c) Use o modelo para estimar o consumo de petróleo em 2002 e 2012.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte tabela que mostra a média mundial de consumo de petróleo desde 1985 até 2010, medida em milhares de barris por dia:
Primeiramente queremos fazer um gráfico relacionando os pontos da tabela e verificar se um modelo linear é apropriado para descrever a tabela.
Para isso, vamos relacionar os pontos na forma no plano cartesiano no formato:
E analisar se eles se comportam como uma reta.
Também queremos fazer um gráfico com uma linha de regressão (essa parte a gente vai utilizar uma ferramenta matemática).
Por fim, com o gráfico gerado pela regressão, deveremos estimar o consumo de petróleo em 2002 e 2012.
Para isso, deveremos saber a equação da curva que será plotada na regressão.
E aí?? Bora lá?? 😉
Passo 2
Bom... marcando todos os pontos dados na tabela, temos:
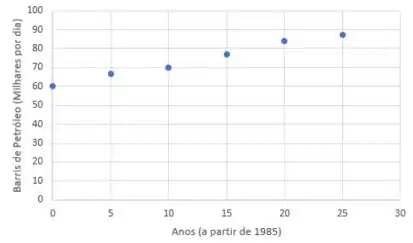
Perceba que analisando o gráfico acima, poderemos concluir que a quantidade de barris de petróleo aumenta de forma linear à medida que se passam os anos.
O modelo de regressão linear representa de forma precisa o consumo real dos barris de petróleo.
Passo 3
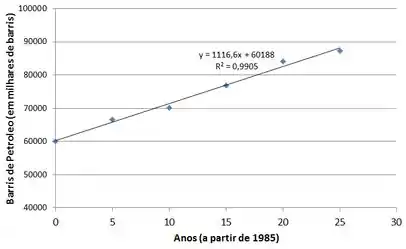
Agora, utilizando uma ferramenta matemática, vamos traçar uma reta de regressão nos pontos e analisar a função gerada:
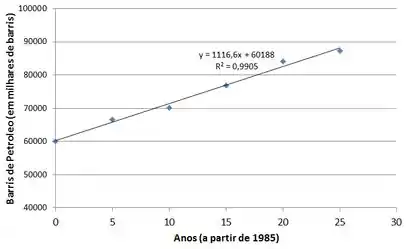
Perceba que a reta descreve bem de forma aproximada o comportamento que estamos analisando!!
Além disso, usamos o coeficiente de determinação para comprovar a qualidade do ajuste, onde varia entre a , sendo quanto mais próximo de , mais exata está a previsão do modelo.
Neste caso encontramos um .
Passo 4
A linha de regressão é representada por:
Onde representa os barris de petróleo e representa os anos.
Para encontrar o consumo de 2002 e de 2012, basta substituir pelo ano que a partir de 1985 na equação acima:
Entendeu direitinho?? Responde aee 😉
Resposta
a)
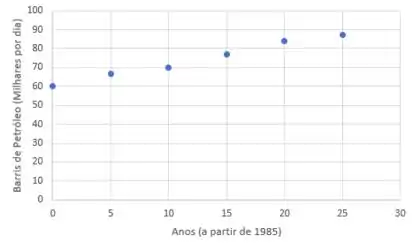
O modelo de regressão linear representa de forma precisa o consumo real dos barris de petróleo.
b)
c)