Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios práticos - Ex. 43

Relacione cada um dos gráficos nos Exercícios 39-46 com a equação apropriada (a)-(l). Há mais equações do que gráficos, portanto algumas equações não serão relacionadas.

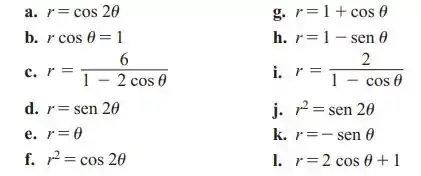
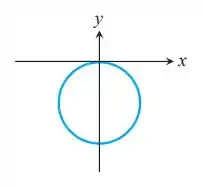
Círculo

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de equações paramétricas e coordenadas polares.

Vamos agora resolver os exercícios práticos sobre gráficos em coordenadas polares.

Para esse gráfico, teremos que sua equação deve ter um dos formatos a seguir:

A distinção entre a utilização de seno ou cosseno está no eixo onde o círculo se estende. Se no eixo x, usamos cosseno. Se no eixo y, usamos seno. O sinal é escolhido de acordo com o semi eixo para o qual se estende o círculo. Como na figura dada, temos que o círculo se estende para o semi eixo negativo de y, a equação associada ao gráfico é:

Passo 2

Como entre todas as possibilidades apresentadas, a única com o formato desejado é o item k (com a = 1), essa equação é associada ao gráfico dado.

E é isso pessoal. Espero que a resolução tenha sido proveitosa para todos. Até mais.

Resposta

Exercícios de Livros Relacionados

Esboce os círculos nos Exercícios 53-56. Dê coordenadas polares para seus centros e identifique seus raios. r = - 2 co s ⁡ θ

O que são coordenadas polares? Quais equações relacionam coordenadas polares a coordenadas cartesianas? Por que você poderia desejar mudar de um sistema de coordenadas para outro?.

Quais consequências a falta de unicidade de coordenadas polares tem para o esboço de gráficos? Dê um exemplo.

Como você determina a área da região 0 ≤ r 1 θ ≤r ≤ r 2 θ , α ≤ θ ≤ β , no plano de coordenadas polares? Dê exemplos.

Sob que condições você pode encontrar o comprimento de uma curva r = f θ , α ≤ θ ≤ β , no plano de coordenadas polares? Dê um exemplo de cálculo típico.