Represente, no ciclo as imagens dos seguintes conjuntos de números reais:
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Neste primeiro passo representaremos as imagens dos dois primeiros conjuntos. Desse modo:
Para o conjunto E, como pertence aos inteiros, teremos como imagem os múltiplos de , assim:
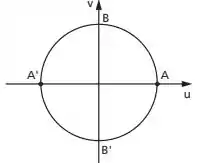
Agora, para o conjunto F, teremos os múltiplos de
Assim:
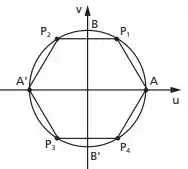
Passo 2
Agora faremos os dois últimos conjuntos.
Comecemos com o conjunto G:
Para esse caso teremos o seguinte conjunto como resolução, pontos diametralmente opostos:
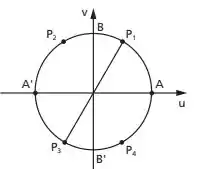
Por fim, o conjunto H:
Neste conjunto teremos pontos nos quatro quadrantes, e estes se darão da seguinte maneira:
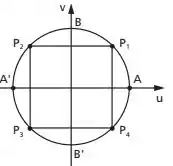
Resposta
Vide passo a passo