Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 54

Represente graficamente as equações dos Exercícios 9-58 seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

54-

Passo 1

Fazendo a primeira derivada temos:

Agora a segunda:

Passo 2

Analisando temos:

Como não tem como ser zero podemos cortar sem se preocupar com ele.

Logo em temos o nosso ponto crítico

Passo 3

Verificando o ponto crítico e vendo se tem pontos de inflexão nós ficamos:

Logo é máximo local.

Ponto de inflexão:

Cortando e separando a variável encontramos inflexão em:

Passo 4

Por não se tratar de um polinômio fracionado não temos assíntotas verticais, verificando agora as horizontais

O que é uma indeterminação , pode-se aplicar L’Hopital:

Agora para menos infinito:

Nesse caso L’Hopital não se aplica pois

Então a função começa em menos infinito e vai até zero.

Passo 5

Fazendo a tabela com os intervalos temos:

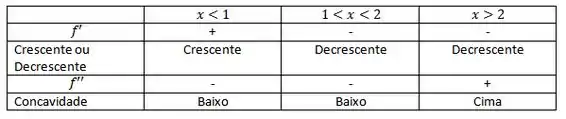
Pontos de teste: 0 1.5 3

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)

Obtenha um gráfico da função racional dada e identifique as coordenadas dos pontos estacionários e de inflexão. Mostre as assíntotas horizontais e verticais e dê suas equações. Identifique (se houver)

Em cada parte, faça um esboço aproximado do gráfico usando assíntotas e limites apropriados, mas não derivadas. Compare seu esboço ao gerado por um recurso gráfico computacional. y = 3 x 2 - 8 x 2 - 4

Em cada parte, faça um esboço aproximado do gráfico usando assíntotas e limites apropriados, mas não derivadas. Compare seu esboço ao gerado por um recurso gráfico computacional. y = 2 x - x 2 x 2 + x

Suponha que f ( x )=P ( x ) / Q ( x ) , em que P e Q são polinômios sem fator comum. Se y=5 for uma assíntota horizontal do gráfico de f , então P e Q terão o mesmo grau.