Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.4 - Ex. 21

Represente graficamente a equação seguindo os passos do procedimento para construção de gráficos da página 237. Inclua as coordenadas de quaisquer pontos extremos e absolutos locais e pontos de inflexão.

y = x 5 - 5 x 4 = x 4 ( x - 5 )

Passo 1

Primeiramente, vemos que a função é um polinômio, logo seu domínio é R .

Vamos calcular a derivada primeira e segunda da função:

y ' = 5 x 4 - 20 x 3 = 5 x 3 ( x - 4 )

y ' ' = 20 x 3 - 60 x 2 = 20 x 2 ( x - 3 )

Passo 2

Vamos encontrar os pontos críticos agora, que são onde a derivada é zero.

y ' = 5 x 3 x - 4 = 0

5 x 3 = 0 → x = 0

x - 4 = 0 → x = 4

E pelo teste da derivada segunda, y ' ' 0 = 0 , e y ' ' 4 = 320 > 0   .

Então, temos um ponto mínimo em 4 ,   y 4 = ( 4 ,   256 )   .

Passo 3

Vamos agora ver os intervalos de crescimento da função.

y ' =   5 x 3 x - 4

Sabemos que a função resulta em zero quando x = 0 e x =   4 . Vejamos então...

Então, a função é crescente em x ∈ ( - ∞ ,   0 ) e ( 4 ,   ∞ ) e decrescente em x ∈   ( 0,4 )   .

Vejamos a concavidade...

Nossa derivada deu y ' ' = 20 x 2 ( x - 3 ) então y ' ' = 0 → x = 0   e   x = 3 ...

Então, a concavidade é para cima em 3 ,   ∞ e para baixo em - ∞ , 0   e   ( 0,3 )

O ponto de inflexão então é: ( 3 ,   - 162 )

Passo 4

Podemos encontrar facilmente ainda o ponto onde a função corta os eixos coordenados:

  • Corta o eixo y em: x = 0 :

    • y 0 =   0 5 - 5 0 4 = 0

    Ponto ( 0,0 ) .

  • Corta o eixo x em: x 4 x - 5 = 0 → x = 0   o u   x = 5

Pontos: 0,0 ,   ( 5,0 )

Passo 5

Juntando as informações, temos o gráfico:

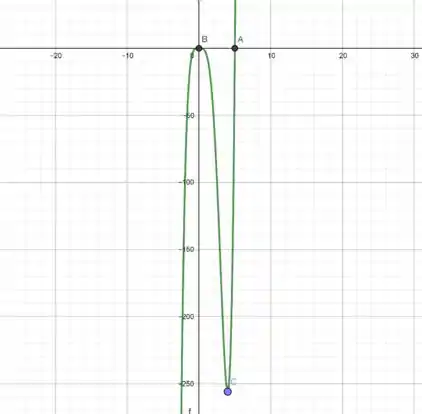
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se f x = sin ⁡ x + ln ⁡ x Encontre f ' ( x ) . Verifique que sua resposta é razoável comparando os gráfico de fef ' .
Uma partícula move-se segunda a lei do movimento s = f ( t ) , t ≥ 0 , em que t é medido em segundos e s em metrosEncontre a velocidade no instante t Qual a velocidade depois de 3 s Quando a partícula
Use o roteiro dessa seção para esboçar a curva. y = x 3 + x
Use o roteiro dessa seção para esboçar a curva. y = x 3 + 6 x 2 + 9 x
Use o roteiro dessa seção para esboçar a curva. y = 2 - 15 x + 9 x 2 - x 3