Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.2 - Ex. 1

Resolva o Exercício 5 da seção6.1 pelo método do invólucro cilíndrico

.

Passo 1

Não entendeu nadinha? Senta aí que você vai ver que não é tão difícil assim.

Ilustrando o que a questão pediu:

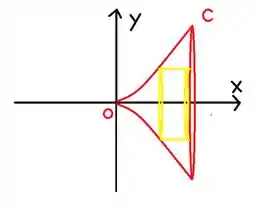
Para o cilindro amarelo, temos o seguinte:

Raio igual a 4   – x

Altura igual a y

Espessura igual a dy( isso significa que a espessura é bem pequena)

Passo 2

Para responder qualquer questão de volume usando esse método é só se ligar na dica.

2 π     r a i o   m é d i o a l t u r a (   e s p e s s u r a )

Então, a nossa integral vai ficar assim:

2 π ∫ 0 8 y 4 - y 2 3 d y  

Como estamos trabalhado com dy, então tudo deve ser escrito em função de y.

Além disso, o limite superior da integral foi encontrado fazendo a intersecção das curvas:

y 2 3 = 4 ⇒ y = 8  

Resolvendo a integral,

2 π ∫ 0 8 4 y - y 5 3 d y  

2 π 4 y 2 2 - 3 8 y 8 3   | 0 8

Substituindo, temos que   V = 64 π

Resposta

64 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que você faça anéis para guardanapos perfurando buracos com diferentes diâmetros através de duas bolas de madeira (as quais têm diferentes diâmetros). Você descobre que ambos os anéis de guard
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. Esboce a região e uma casca típica. y = x ² , y = 0 ,