Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.7 - Ex. 4
Ache o valor de que satisfaz o teorema do valor médio para integrais para a integral a seguir. Faça uma figura ilustrando a aplicação do teorema.
Passo 1
O teorema do valor médio para integrais diz que se temos uma função contínua num intervalo , vai existir um número dentro do intervalo para o qual:
Sabemos que a integral é a área abaixo do gráfico de uma função em dado intervalo, então o que o teorema diz é que existe um número dentro do intervalo para o qual a integral é igual a área de um retângulo com base e com altura igual ao valor da função naquele ponto.
Pra acharmos qual é esse ponto , basta substituirmos diretamente os valores no teorema.
Passo 2
Temos então:
Mas , então isso nos leva a:
Passo 3
Para ilustrar o teorema, esboçamos o gráfico da função no intervalo e mostramos o retângulo com base na semi-reta que vai de a e altura igual a .
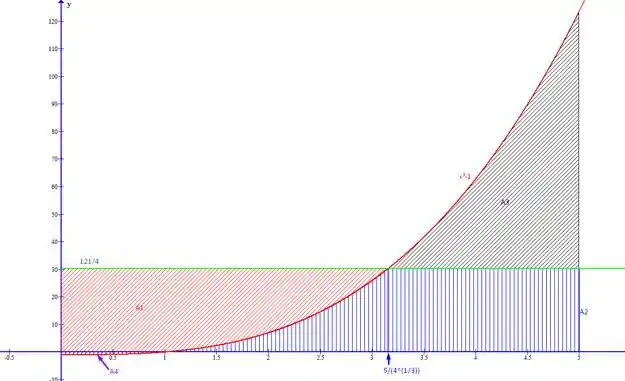
Note que a integral tem valor ( com valor negativo pois está abaixo do eixo x) e o retângulo tem área , e se essas duas áreas são iguais isso implica que .