Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.8 - Ex. 105
Resolva os problemas de valor inicial nos Exercícios 91-112.
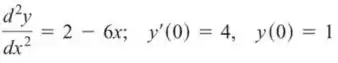
Passo 1
O primeiro passo que pode ser feito para encontrar a solução do P.V.I. é integrar a expressão diferencial que o enunciado fornece.
Em seguida, deve aplicar as condições iniciais para a primeira derivada a fim de encontrar o valor da primeira constante que irá aparecer.
Após isso, deve-se integrar novamente a equação, cujo resultado da integral irá nos dar a função primitiva da derivada de segunda ordem e na qual podemos substituir os outros valores da condição inicial a fim de encontrarmos a equação desejada.
Passo 2
Portanto,
Passo 3
O exercício nos dá uma condição inicial na qual diz que quando . Com esses valores é possível descobrir o valor da primeira constante e, assim, descobrir a equação que representa a primeira derivada. Logo:
Então, a equação da primeira derivada é .
Passo 4
Em seguida, deve-se integrar novamente para encontrar a equação da função primitiva:
Passo 5
O exercício nos dá outra condição inicial na qual diz que quando . Com esses valores é possível descobrir o valor da segunda constante e, assim, saber qual é a equação final. Logo:
Então, a equação correta é .
Resposta
A solução do P.V.I. é .