Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.7 - Ex. 36
Responde o exercício se um pedaço estiver dobrado no formato de um quadrado e o outro num formato de um círculo.
Passo 1
Opa, tranquilo? Antes de mais nada vamos relembrar o que o exercício 35 pedia!
O enunciado nos disse que um pedaço de fio com de comprimento foi cortado em duas partes. Uma parte foi dobrada no formato de um quadrado e a outra foi dobrada na forma de um círculo.
O objetivo aqui é encontrar a área total máxima e mínima dessas figuras. Este é claramente um problema de otimização.
Você tem ideia de como fazemos isso?
Neste problema, precisamos desenvolver a equação da área em função das variáveis que queremos otimizar e também uma equação que relacione essas variáveis.
Aí, substituímos uma equação na outra e aplicamos a metodologia que usamos para encontrar os pontos críticos de uma função: derivamos e igualamos a zero.
Sacou? Bora começar!
Esboçando o desenho com as novas informações:
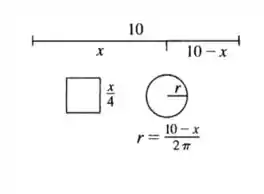
Isolar o raio nos ajuda a resolver porque faz com que todas as contas fiquem em função de , e deixa nossa vida muito mais fácil!
Passo 2
Assim como no exercício anterior, a gente precisa achar as áreas totais máxima e mínima, então:
- Temos um quadrado de lado , sua área é
- Área do circulo é , o raio que já calculamos, vamos só substituir:
Agora é só somar as duas áreas, assim:
Abrindo o produto notável:
Passo 3
Derivando e igualando a zero para encontrar os valores extremos:
Vamos derivar então:
Vamos igualar a e juntar as variáveis :
E finalmente encontrado o valor de :
Passo 4
Como pode variar entre zero e dez, substituímos esses dois valores além do encontrado para encontrar seus valores extremos e achar os pontos máximos e mínimos:
Assim nós chegamos nas nossas repostas:
Item (a): área máxima encontrada acontece quando , e vale , ou seja, toda a corda é usada para o círculo.
Item (b): área mínima encontrada acontece quando , e vale .
Resposta
Item (a): área máxima: .
Item (b): área mínima: .