Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 15
Sefor a função considerada no Exemplo 3, use um sistema de computação algébrica para calcular então faça seu gráfico para confirmar que todos os valores máximos e mínimos são como dados no exemplo. Calcule e use-a para estimar os intervalos de concavidade e pontos de inflexão.
Passo 1
A função que temos no Exemplo 3 é
O enunciado nos pede para usar um sistema de computação algébrica para calcular a derivada da função, ou seja, não vamos precisar calcular essa derivada na mão.Depois é pedido para se fazer o gráfico da derivada para encontrar os valores máximos e mínimos.
Lembrando que os máximos ocorrem quando a primeira derivada troca de sinal, onde ela era antes positiva e depois passa a ser negativa. Já os mínimos ocorrem quando a primeira derivada troca de sinal, onde ela antes era negativa e passa a ser positiva.
Por fim, vamos calcular a segunda derivada e estimar os intervalos de concavidade e pontos de inflexão.A função é côncava para cima quando é positiva
A função é côncava para baixo quando é negativa
E a função possui um ponto de inflexão quando troca de sinal.
Passo 2
Como o enunciado nos pede e , então usaremos um sistema de computação algébrica pra resolver esse monstrinho, então chegamos no seguinte resultado:
Passo 3
Plotando diferentes intervalos pra , a gente consegue ter uma boa ideia de qual é a melhor visão, então temos as seguintes janelas:
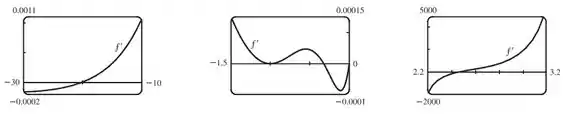
Pelos gráficos de , a gente pode ver que os pontos críticos estão em e como é estimado no Exemplo 3.
Pontos críticos são aquelas onde a derivada é igual à zero ou não existe.
No entanto, o ponto , apesar de ser um ponto crítico, não é um ponto de máximo ou mínimo, pois a derivada não troca de sinal nele.
O ponto é um ponto de mínimo, pois a derivada antes dele é negativa e depois é positiva.O ponto é um ponto de máximo, pois a derivada antes dele é positiva e depois é negativa.
O ponto é um ponto de mínimo, pois a derivada antes dele é negativa e depois é positiva.
Passo 4
Agora plotando com diferentes intervalos pra , a gente tem as seguintes janelas:
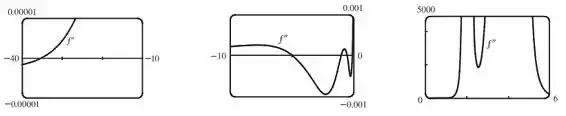
Por esses gráficos conseguimos visualizar que é côncava para cima em
e côncava para baixo em
Para os pontos mais próximos da origem, é necessário aumentar o zoom para verificar onde a segunda derivada troca de sinal.
Agora falta achar os pontos de inflexão.
Olhando os gráficos de , n��s já vemos os pontos em em que a função troca o sinal, que caracteriza pontos de inflexão, são eles:
, então substituindo esses valores de em , achamos as coordenadas .
Então, os pontos são aproximadamente e .
Resposta
Pontos de Mínimo
Ponto de Máximo
Pontos de Inflexão