Seja .
(a) Calcule .
(b) Calcule .
(c) Determine e esboce o domínio de .
(d) Determine a imagem de .
Passo 1
Falaee, belezinha?? Bom... o enunciado nos deu a seguinte expressão:
Queremos primeiramente calcular e . Para isso, basta compararmos os valores de e que nos foram dados e substituir na função.
Em seguida, deveremos determinar o domínio e a imagem dessa função.
Para encontrar o domínio, precisamos determinar os valores de e que não causam problemas (divisão por zero, raízes de números negativos, logaritmos de números não positivos).
Já para encontrarmos a imagem, devemos buscar os valores de que a função pode assumir ao avaliar todos os e do domínio.
Passo 2
Vamos primeiro calcular .
Assim, sabemos que:
Logo, substituindo na função, obtemos:
, já que .
Passo 3
Agora vamos calcular .
Assim, sabemos que:
Logo, substituindo na função, obtemos:
, já que .
Passo 4
Queremos determinar o domínio de . Ou seja, queremos saber que valores de podem ser usados para que seja real.
Para definir o domínio, é melhor olhar para as restrições.
Sabemos que .
Assim, temos que:
Logo, o domínio de é definido por . É a área hachurada abaixo:
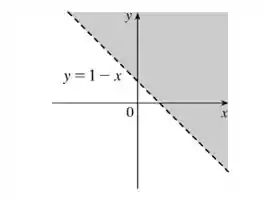
Passo 5
Queremos determinar a imagem de . Ou seja, se usarmos todas as combinações possíveis de valores do domínio, quais serão todos os valores possíveis de ?
Assim como fizemos para o domínio, vamos dar uma olhada nas restrições.
Não há restrições!
Como pode ser qualquer número em , a imagem de é qualquer número real.
Resposta
(a)
(b)
(c)
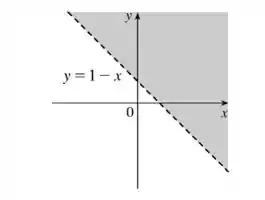
(d)