Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 7.1 - Ex. 9
Desenhe a imagem.
Passo 1
Essa é uma questão bem interessante em que temos que desenhar a imagem da curva
Note que podemos escrever e parametricamente como função de :
Agora vem o pulo do gato: observe que
Aí você deve estar pensando em desenhar a parábola completa e problema resolvido, certo? Errado!
Passo 2
Nós achamos que a imagem da curva está contida na parábola , mas não podemos afirmar que a curva será a parábola toda.
Lembre-se que
Assim, temos que
Portanto, a imagem da curva será a parte da parábola restrita ao intervalo .
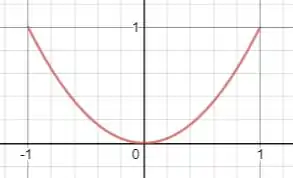
Resposta
Esboço de curva.
Exercícios de Livros Relacionados
Determine o conjunto dos pontos de acumulação do conjunto dado.e) x , y ∈ I R 2 |x = 1 ,1y2
Seja F um subconjunto do I R 2 . Dizemos que F é um conjunto fechado se o conjunto de todos os ( x , y ) não-pertencentes a F for aberto. Verifique quais dos conjuntos a seguir são fechados.g) x , y ∈
Determine o conjunto dos pontos de acumulação do conjunto dado.f) x , y ∈ I R 2 |xeyr a c i o n a i s
Seja F um subconjunto do I R 2 . Dizemos que F é um conjunto fechado se o conjunto de todos os ( x , y ) não-pertencentes a F for aberto. Verifique quais dos conjuntos a seguir são fechados.b) x , y ∈
Seja F um subconjunto do I R 2 . Dizemos que F é um conjunto fechado se o conjunto de todos os ( x , y ) não-pertencentes a F for aberto. Verifique quais dos conjuntos a seguir são fechados.d) x , y ∈