Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 34

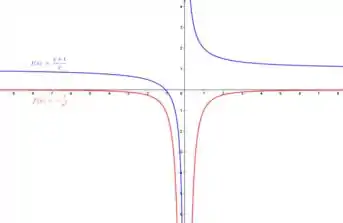
a) Seja f x = x + 1 x , encontre f ' x .

b) Verifique se sua resposta na parte (a) foi razoável, comparando os gráficos de f   e f '

Passo 1

Fala aí! tudo certinho? 😉

Nesse problema foi dada a função f x = x + 1 x e nosso objetivo é calcular f ' x e comparar os gráficos de f e f ' .

Tem ideia de como fazer isso? 🤔

Para obter a função f ' x , vamos usar a definição pelo limite

f ' x =   lim h → 0 ⁡ f x + h - f ( x ) h

Sacou? Bora começar! 😉

Passo 2

Pela definição de derivada, temos

f ' x =   lim h → 0 ⁡ f x + h - f ( x ) h

Vamos trazer isso pro nosso caso agora

f x + h = x + h + 1 x + h

Substituindo a função...

f ' x = lim h → 0 ⁡ x + h + 1 x + h - x + 1 x h

f ' x = lim h → 0 ⁡ x x + h + 1 - ( x + h ) ( x + 1 ) ( x + h ) ( x ) h

f ' x = lim h → 0 ⁡ x 2 + x h + x - x 2 - x - h x - h ( x 2 + h x ) ∙ 1 h

f ' x = lim h → 0 ⁡ - 1 x 2 + h x

Calculando o limite, chegamos em

f ' x = - 1 x 2

Derivada encontrada!

Passo 3

Vamos dar uma olhada nos gráficos agora...

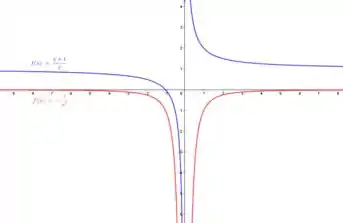
Vemos que a resposta encontrada para f ' foi razoável, pois a função f é sempre decrescente e a derivada é sempre negativa.

Vemos também que não existe ponto em que a reta tangente ao gráfico de f é horizontal, e a derivada nunca é zero, o que justifica esse fato.

E aí! entendeu tudo? Responde Aí! 😉

Resposta

f ' x = - 1 x 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use os gráficos dados para estimar o valor de cada derivada. Esboce então o gráfico de f ' . b) f ' ( - 2 )
Use os gráficos dados para estimar o valor de cada derivada. Esboce então o gráfico de f ' . c) f ' ( 2 )
Use os gráficos dados para estimar o valor de cada derivada. f ' ( - 3 )
Use os gráficos dados para estimar o valor de cada derivada. Esboce então o gráfico de f ' . c) f ' - 1
Use os gráficos dados para estimar o valor de cada derivada. f ' ( 7 )