Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.10 - Ex. 6

Seja f x = x 2 - 1 ,   s e   x ≤ 1 1 - x 2 ,   s e   x > 1

  1. Esboçar o gráfico de f ;
  2. Verificar se f é contínua nos pontos - 1 e 1 ;
  3. Calcular f ' - 1 - ,   f ' - 1 + ,   f ' 1 -   e   f ' ( 1 + ) ;
  4. Calcular f ' ( x ) , obter o seu domínio e esboçar o gráfico.

Passo 1

Pessoal, na letra (a) queremos o esboço do gráfico da f . Assim, temos:

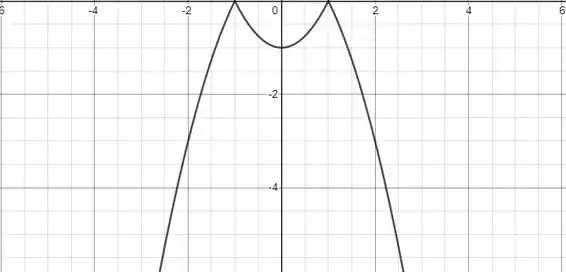
Passo 2

Para descobrirmos se uma função é contínua, basta analisarmos o limite pela esquerda e pela direita. Assim, vamos analisar para x = 1 :

lim x → 1 + ⁡ f x = lim x → 1 + ⁡ 1 - x 2 = 0 = f 1

lim x → 1 - ⁡ f x = lim x → 1 - ⁡ x 2 - 1 = 0 = f 1

Agora para x = - 1 :

lim x → - 1 + ⁡ f x = lim x → - 1 + ⁡ 1 - x 2 = 0 = f - 1

lim x → - 1 - ⁡ f x = lim x → - 1 - ⁡ 1 - x 2 = 0 = f - 1

Logo, f é contínua em x = 1 e x = - 1 .

Passo 3

Vamos agora calcular as derivadas laterais! Se a função y = f ( x ) está definida em x 1 , então as derivadas à direita e a esquerda de f em x 1 , denotadas por f + ' ( x 1 ) e f - ' ( x 1 ) são definidas por:

f + ' x 1 = lim ∆ x → 0 + ⁡ f x 1 + ∆ x - f x 1 ∆ x = lim x → x 1 + ⁡ f x - f x 1 x - x 1

f - ' x 1 = lim ∆ x → 0 - ⁡ f x 1 + ∆ x - f x 1 ∆ x = lim x → x 1 - ⁡ f x - f x 1 x - x 1

Uma função é derivável em um ponto, quando as derivadas à direita e à esquerda nesse ponto existem e são iguais. Assim, temos:

f ' - 1 + = lim ∆ x → 0 + ⁡ - 1 + ∆ x 2 - 1 - - 1 2 + 1 ∆ x = - 2

f ' - 1 - = lim ∆ x → 0 - ⁡ 1 - - 1 + ∆ x 2 - 1 + - 1 2 ∆ x = 2

f ' 1 + = lim ∆ x → 0 + ⁡ 1 - 1 + ∆ x 2 - 1 + 1 2 ∆ x = - 2

f ' 1 - = lim ∆ x → 0 - ⁡ 1 + ∆ x 2 - 1 - 1 2 + 1 ∆ x = 2

Passo 4

Vamos calcular a derivada de f ( x ) !

f ' x = 2 x ,   s e   x < 1 - 2 x ,   s e   x > 1

Segue o gráfico

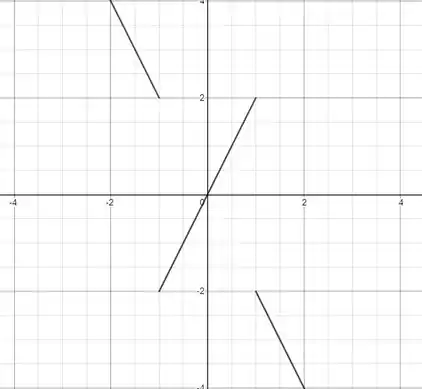
O domínio da função derivada é D = R - { - 1,1 } .

Resposta

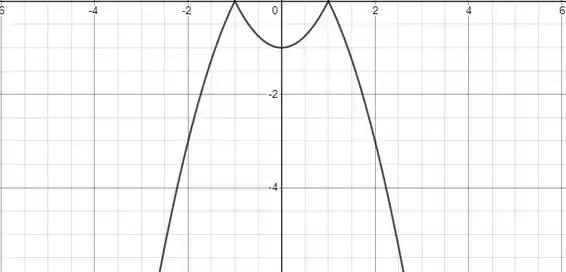
  2. f é contínua em x = 1 e x = - 1 .
  3. f ' - 1 + = - 2 ;   f ' - 1 - = 2 ;   f ' 1 + = - 2 ;   f ' 1 - = 2 .
  4. A função derivada é igual a

f ' x = 2 x ,   s e   x < 1 - 2 x ,   s e   x > 1

Com domínio D = R - { - 1,1 }

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as derivadas à direita e à esquerda como limites para mostrar que a função não é derivável no ponto P.
Calcule as derivadas à direita e à esquerda como limites para mostrar que a função não é derivável no ponto P.
Calcule as derivadas à direita e à esquerda como limites para mostrar que a função não é derivável no ponto P.
Encontrar as derivadas laterais das seguintes funções, nos pontos indicados. Encontrar os intervalos onde f ' x0 e f ' x0 .
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico. f x = 1 - x 2 ,x1 0 , x ≤ 1