Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.2 - Ex. 38
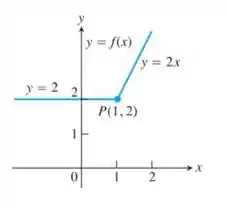
Calcule as derivadas à direita e à esquerda como limites para mostrar que a função não é derivável no ponto P.
Passo 1
Primeiro, devemos saber que definimos a derivada à esquerda de uma função como sendo:
Já a derivada à direita é definida como:
Passo 2
No ponto P, temos
Logo, calcularemos as derivadas laterais utilizando como
Derivada à esquerda:
Derivando à direita:
Passo 3
Como as derivadas laterais são diferentes, podemos afirmar que a função não é derivável no ponto P.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Jared Fogle, também conhecido como o “garoto propaganda do Subway”, pesava 193 k g em 1997 , antes de perder mais 108 k g em 12 meses. Um gráfico mostrando a perde de peso, possivelmente dramática, é
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico. f x = x , s ex1 2 x - 1 , s ex ≥ 1
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico. f x = 2 | x - 3 |
Seja f x = x 2 - 1 ,s ex ≤ 1 1 - x 2 ,s ex1 Esboçar o gráfico de f ;Verificar se f é contínua nos pontos - 1 e 1 ;Calcular f ' - 1 - ,f ' - 1 + ,f ' 1 -ef ' ( 1 + ) ;Calcular f ' ( x ) , obter o seu d
Nos exercícios 1 a 5 calcular as derivadas laterais nos pontos onde a função não é derivável. Esboçar gráfico. f x = 2 - x 2 ,x- 2 - 2 , x ≤ 2 2 x - 6 ,x2