Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.Revisão - Ex. 46
- Gere o gráfico de
No intervalo de e faça uma conjectura sobre a localização e a natureza de todos os pontos críticos.
- Encontr a localização exata de todos os pontos críticos e classifique-os como máximos e mínimos relativos, ou nenhum dos dois.
- Confirme os resultados de (b) fazendo gráficos de partes de em intervalos apropriados. [nota: Não é possível encontrar uma única janela na qual sejam visíveis todos os pontos críticos].
No intervalo de e faça uma conjectura sobre a localização e a natureza de todos os pontos críticos.
Passo 1
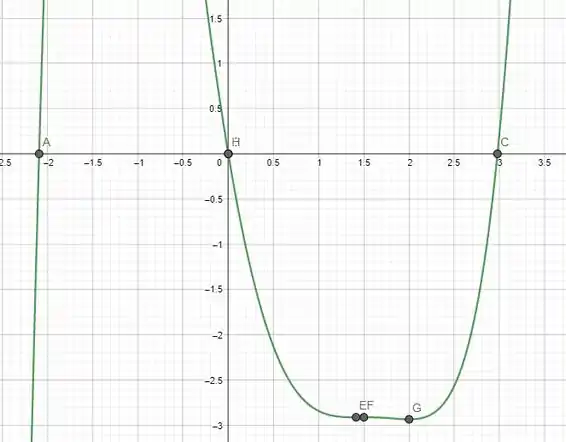
- O execicio pede para que construamos um gráfico da função utilizando ferramentas gráficas:
- Vamos encontrar os pontos críticios pelo teste da segunda derivada:
- O exercício pede para confirmar os resultados observando o gráfico em intervalos menores:
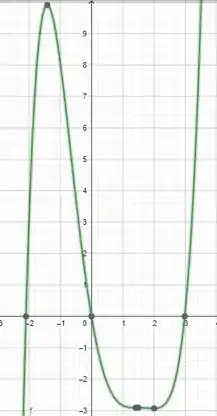
Conforme podemos observar os pontos marcados no gráfico, vemos que mudanças acontecem em: , , e .
Passo 2
Derivando a função:
Fatorando a rais bi quadarada em raiz cúbica, temos:
A primeira raíz zera em .
Vamos resolver o restante da função, ficamos com :
Para retirar os decimais, vamos multiplicar tudo por 10:
Fatorando o termo 5, em comum a todos os termos, ficamos com:
Vamos lidar com a função interna a fatoração:
Podemos reescrever assim:
Isolando os termos em comum:
Agora, conseguimos calcular as raízes restantes , quando:
Quando :
As raízes desse problema são:
Agora, calculamos a segunda derivada:
Aplicando as raízes da segunda derivada na primeira derivada, temos:
Passo 3
