Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.6 - Ex. 24

Seja s t = t e t a função posição de uma partícula movendo-se ao longo de um eixo coordenado, onde s está em metros e t está em segundos. Use um recurso gráfico computacional para gerar os gráficos de s t , v t e a t para t ≥ 0 e use os gráficos quando for necessário.

  1. Use o gráfico apropriado para fazer uma estimativa do instante em que ocorre a primeira reversão do sentido do movimento da partícula e, então, encontre esse instante.
  2. Encontre a posição exata da primeira reversão do sentido do movimento da partícula.
  3. Use o gráfico apropriado para fazer estimativas dos intervalos onde a partícula está aumentando e diminuindo sua velocidade, e depois, encontre esses intervalos.

Passo 1

Para acha a função velocidade é só derivar a função posição, vamos lá:

v t = s ' t = 1 ⋅ e t - t ⋅ e t ⋅ 1 e t 2 = e t - t e t e 2 t = e t 1 - t e 2 t = 1 - t e t

E a função aceleração é a derivada da função velocidade, vamos então derivar:

a t = v ' t = 0 - 1 e t - 1 - t ⋅ e t ⋅ 1 e t 2 = - e t - 1 - t e t e 2 t = - e t - e t + t e t e 2 t =

= - 2 e t + t e t e 2 t = e t - 2 + t e 2 t = - 2 + t e t

Temos as três expressões, vamos colocar elas em um gráfico, com s t de vermelho, v t de azul e a t de verde:

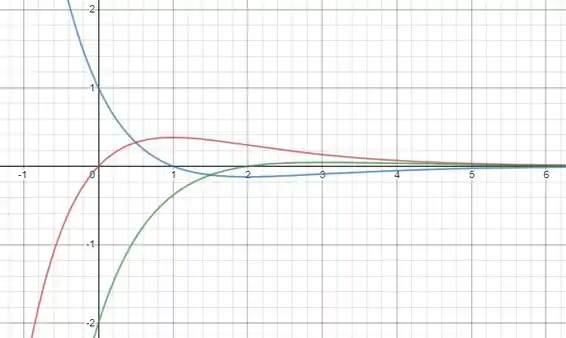
Passo 2

  1. Analisando o gráfico de s t vemos que a primeira reversão do sentido do movimento da partícula se dá mais ou menos em x = 1 , vamos encontrar esse instante fazendo v t = 0 :

    2. 1 - t e t = 0 → 1 - t = 0 → t = 1

    Passo 3

  2. Para encontrar a posição exata da primeira reversão do sentido do movimento da partícula é só achar s 1 :

    3. s 1 = 1 e 1 = 1 e

    Passo 4

  3. Vamos usar os gráficos da velocidade e da aceleração para fazer estimativas dos intervalos, ela está aumentando se a velocidade e a aceleração tiverem o mesmo sinal; e diminuindo se a velocidade e a aceleração tiverem sinais opostos.

Pelos gráficos, vemos que a partícula deve está acelerando em 1 < t < 2 e desacelerando em 0 < t < 1 e t > 2 .

Temos que a velocidade v t > 0 quando 0 < t < 1 e v t < 0 quando t > 1 .

Vamos ver onde a t = 0 :

- 2 + t e t = 0 → - 2 + t = 0 → t = 2

Já com a aceleração temos que a t > 0 quando t > 15 e a t < 0 quando 0 < t < 15 .

Assim a partícula está acelerando em 1 < t < 2 e desacelerando em 0 < t < 1 e t > 2 .

Resposta

  1. t = 1
  2. s 1 = 1 e
  3. A partícula está acelerando em 1 < t < 2 e desacelerando em 0 < t < 1 e t > 2 .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o roteiro desta seção para esboçar a curva: y = 1 5 x 5 - 8 3 x 3 + 16 x
Use o roteiro desta seção para esboçar a curva: y = 4 - x 2 5
Use o roteiro desta seção para esboçar a curva: y = x 2 - 4 x 2 - 2 x
Use o roteiro desta seção para esboçar a curva: y = x - x 2 2 - 3 x + x 2
Um modelo para dispersão de um rumor é dado pela equação p t = 1 1 + a e - k t Onde p ( t ) é a proporção da população que já ouviu o boato no tempo t e a e k são constantes positivas.Quando a metade