Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.Revisão - Ex. 29
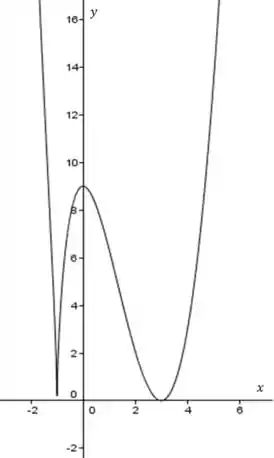
Nos Exercícios de 13 a 32, faça um esboço do gráfico da função dada, determinando primeiro o seguinte: os extremos relativos de ; os pontos de inflexão do gráfico de ; os intervalos nos quais é crescente e aqueles onde é decrescente; onde o gráfico é côncavo para cima e onde é côncavo para baixo; a inclinação das tangente inflexionais, as assíntotas horizontal, vertical e oblíqua, se existirem.
29.
Passo 1
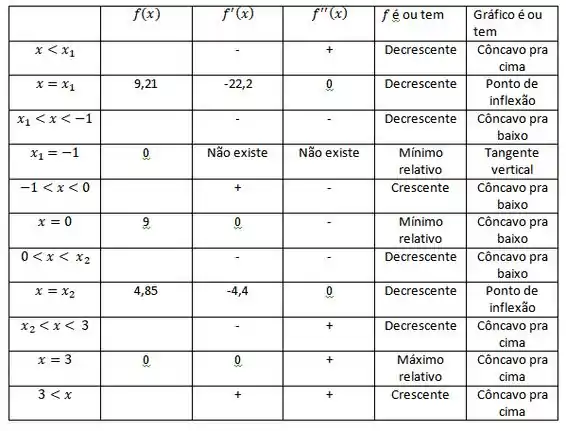
Vamos fazer os testes da primeira e segunda derivada, analisar os pontos, daí organizamos uma tabela. No fim, fazemos o esboço do gráfico.
Passo 2
Para determinar tudo que a questão pede, precisamos da primeira derivada da função :
Colocando em evidência:
Igualando a zero:
ou
Vamos guardar esse resultado pra analisar
Passo 3
Também precisamos da segunda derivada:
Colocando em evidência:
Igualando a zero:
ou
Passo 4
Agora vamos avaliar o que acontece com , e quando se aproxima ou é igual aos valores que achamos...
Para :
pode assumir valores, não precisamos dizer quais.
é negativa
é positiva
Nessa parte, é decrescente e côncava pra cima.
Passo 5
Para
Nessa parte, é decrescente e temos um ponto de inflexão (a concavidade vai mudar).
Passo 6
Para
pode assumir valores, não precisamos dizer quais.
é negativa
é negativa
Nessa parte, é decrescente e côncava para baixo.
Passo 7
Para
não existe
não existe
Nessa parte, tem um mínimo relativo e uma tangente vertical.
Passo 8
Para
pode assumir valores, não precisamos dizer quais.
é positiva
é negativa
Nessa parte, é crescente e côncava para baixo.
Passo 9
Para
é negativa
Nessa parte, tem um mínimo relativo e é côncava para baixo.
Passo 10
Para
pode assumir valores, não precisamos dizer quais.
é negativa
é negativa
Nessa parte, é decrescente e côncava para baixo.
Passo 11
Para
Nessa parte, é decrescente e tem um ponto de inflexão.
Passo 12
Para
pode assumir valores, não precisamos dizer quais.
é negativa
é positiva
Nessa parte, é decrescente e côncava para cima.
Passo 13
Para
é positiva
Nessa parte, tem máximo relativo e é côncava para cima.
Passo 14
Para
pode assumir valores, não precisamos dizer quais.
é positiva
é positiva
Nessa parte, é crescente e côncava para cima.
Passo 15
O esboço fica assim:
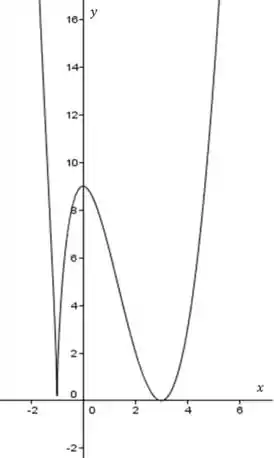
Resposta
Esboço:
