Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 18
Seja um polinômio de grau . Prove:
Sugestão: Dividindo-se por , obtém-se um quociente e um resto , constante, tal que .
Passo 1
Fala, galera. Vamos resolver essa questão!
O enunciado pediu pra gente provar que é raiz de , o que equivale a dizer que é divisível por . Mas quando é que um número é dito divisível por outro? Quando o resto da divisão é igual a zero.
É isso que nós vamos entender nessa questão para conseguir provar que a divisão de por nos fornece um quociente , que é uma função, e um resto , que é uma constante e, nesse caso, igual a zero.
Vamos lá!
Passo 2
Pra começo de conversa, vamos conversar sobre o que significa dizer que uma coisa é divisível por outra. Vamos com um exemplo! Se calculamos , temos,
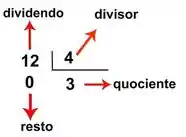
Repara que o nosso resto é zero, ou seja, 12 é divisível por 4. Podemos escrever essa conta como uma multiplicação, fica assim:
E se o resto for diferente de zero? Neste caso, um número não é divisível por outro. Por exemplo, não é divisível por :
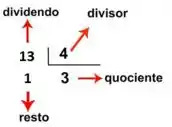
Escrevendo como uma multiplicação, temos:
Vemos então que, pra dizermos que uma coisa é divisível pela outra, o resto da divisão tem que ser zero, como vimos no passo .
A ideia pra funções é a mesma da ideia para números. Então fica assim:
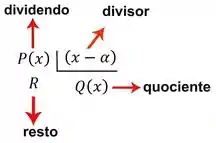
Escrevendo como multiplicação, ficamos com:
Então, temos que provar que .
Passo 3
Para provar que , temos que buscar um valor para substituir em , onde a gente saiba o resultado. Mas lembra que o enunciado mencionou que é raíz de , ou seja,
Agora vamos substituir na expressão que encontramos,
Como todo número multiplicado por zero é zero, temos:
Opa, olha só no que chegamos: o resto da nossa divisão é igual a quando é raíz do polinômio. E tá na mão! Provamos que o resto da nossa divisão é zero!