Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.2 - Ex. 20d
Resolva a inequação.
Passo 1
Do exercício , sabemos que o polinômio pode ser fatorado da seguinte forma:
Passo 2
Agora vamos fazer o estudo de cada termo separadamente.
- Para
- Para
- Para
Antes de , por exemplo , o termo assume valores negativos. E depois, como por exemplo em , assume valores positivos.
Antes de , por exemplo , o termo assume valores negativos. E depois, como por exemplo em , assume valores positivos.
Antes de , por exemplo , o termo assume valores negativos. E depois, como por exemplo em , assume valores positivos.
Lembrando que a multiplicação de sinais é feita de dois a dois:
Agora é só analisar os intervalos todos juntos.
Vamos resumir isso em um desenho:
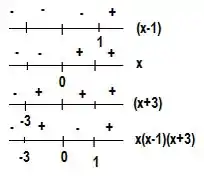
A multiplicação desses fatores está indicado na última linha.
Passo 3
O intervalo de interesse é onde esse polinômio assume valores mmenores do que zero, então os valores de que satisfazem essa inequação serão:
Beleza? Vamos pra próxima?