Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.11 - Ex. 64

  1. Seja   Q x =   b 0 + b 1 x - a +   b 2 x - a 2 uma aproximação quadrática de f(x) quando x = a, com as seguintes propriedades:

    2. i) Q a = f ( a )

    ii) Q ' a = f ' ( a )

    iii) Q ' ' a = f ' ' ( a )

    Determine os coeficientes b 0 , b 1 e b 2 .

  2. Determine a aproximação quadrática para f x = 1 / ( 1 - x ) em x = 0.

  3. Esboce o gráfico de f x = 1 / ( 1 - x ) e sua aproximação quadrática em x =0. Depois, amplie os dois gráficos no ponto (0, 1 ). Comente o que você observa.

  4. Determine a aproximação quadrática para g(x) = 1/x em x = 1. Trace em um único gráfico g e sua aproximação quadrática. Comente o que observa.

  5. Determine a aproximação quadrática de h x = 1 + x   em x = 0 .Trace em um mesmo gráfico h e sua aproximação quadrática. Comente o que observa.

  6. Quais são as linearizações de f, g e h nos respectivos pontos dos itens (b), (d) e (e)?

Passo 1

Vamos resolver item por vez...

Item a): Temos que:

  1. Q a =   b 0 + b 1 a - a +   b 2 a - a 2 → Q a =   b 0 = f ( a )
  2. Q’(x) =   b 1 + 2 b 2 x - a , então: Q ' a = b 1 = f ' ( a )
  3. Q ' ' x = 2 b 2 , então Q ' ' a = 2 b 2 = f ' a → b 2 = f ' a 2

E assim temos os coeficientes pedidos.

Passo 2

  1. Determine a aproximação quadrática para f x = 1 / ( 1 - x ) em x = 0.

Vamos calcular os coeficientes de acordo com o item anterior:

Temos que:

f x = 1 1 - x - 1 e então: f 0 = 1 1 - 0 - 1 = 1 = b 0

f ' x =   - 1 1 - x - 2 - 1 = 1 - x - 2 , então: f ' 0 = 1 - 0 - 2 = 1 = b 1

f ' ' x - 2 1 - x - 3 - 1 = 2 1 - x - 3 , então: f ' ' 0 = 2 1 - 0 - 3 = 2 = 2 b 2 → b 2 = 1

Logo, nossa aproximação quadrática é dada por: Q x = 1 + x + x 2

Passo 3

C)

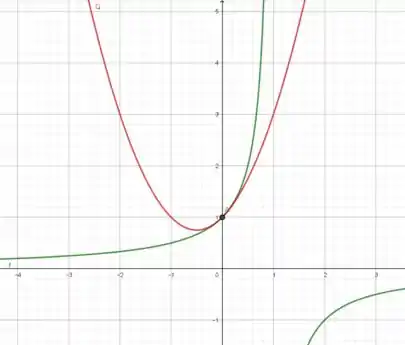
No ponto (0,1) os gráficos se tornam indistinguíveis, o que nos mostra que a aproximação quadrática está correta.

Passo 4

d) Vamos proceder igual ao item anterior:

g x = 1 x - 1   ,   então, g 1 = 1 = b 0

g ' x =   - 1 x - 2   , então g ' 1 =   - 1 = b 1

g ' ' ( x ) = 2 x - 3 , então g ' ' 1 = 2 = 2 b 2 → b 2 = 1

Então, a aproximação quadrática é dada por: Q x = 1 - x - 1 + ( x - 1 ) 2 .

Temos o gráfico:

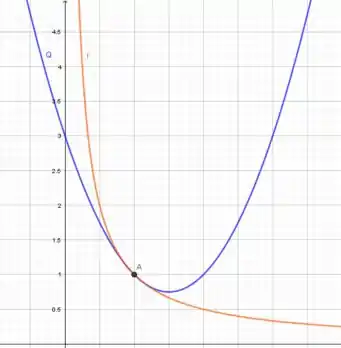
Vemos que no ponto (1,1) os gráficos são indistinguíveis, logo a aproximação quadrática está correta.

Passo 5

Temos que:

h x = 1 + x 1 2 , então: h 0 = 1 = b 0

h ' x = 1 + x - 1 2 2 , então: h ' 0 = 1 2 = b 1  

h ' ' x =   - 1 + x - 3 2 4 , então: h ' ' 0 =   - 1 4 = 2 b 2 → b 2 =   - 1 8

Então a aproximação quadrática é dada por: Q x = 1 + 1 2 x - 1 8 x 2

Teremos os gráficos:

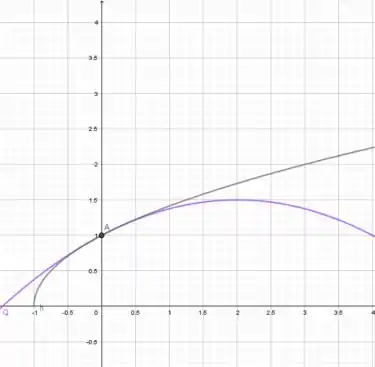
Vemos que no ponto (0,1) os gráficos são indistinguíveis, logo a aproximação quadrática está correta.

Passo 6

A linearização de uma função diferenciável é dada por:

L x = f a + f ' a x - a = b 0 + b 1 ( x - a )

Então:

  • f:   L x = 1 + x
  • g: L x = 1 - ( x - 1 )
  • h: L x = 1 + x 2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O lado x de um cubo é medido com um erro de no máximo 0,5%. Qual é a porcentagem máxima de erro correspondente no cálculo:da área de superfície? do volume?
Um agrimensor, a 30 pés da base de um edifício, mede o ângulo de elevação até o topo do edifício como sendo de 75°. Quão exata deve ser a medição desse ângulo para que o erro percentual na estimativa
Determine a linearização de f x = 2 x em x = 0. Depois, arredonde seus coeficientes para duas casas decimais. Trace em um mesmo gráfico a linearização e a função para - 3
Determine a linearização de f x = log 3 ⁡ x em x = 3. Depois, arredonde seus coeficientes para duas casas decimais. Trace em um mesmo gráfico a linearização e a função para 0 ≤ x ≤ 8e2 ≤ x ≤ 4 .