Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.11 - Ex. 66
- Determine a linearização de em x = 3. Depois, arredonde seus coeficientes para duas casas decimais.
- Trace em um mesmo gráfico a linearização e a função para .
Passo 1
- A linearização de uma função diferenciável é dada por:
Nesse caso temos:
Daí:
Arredondando:
Passo 2
Gráfico:
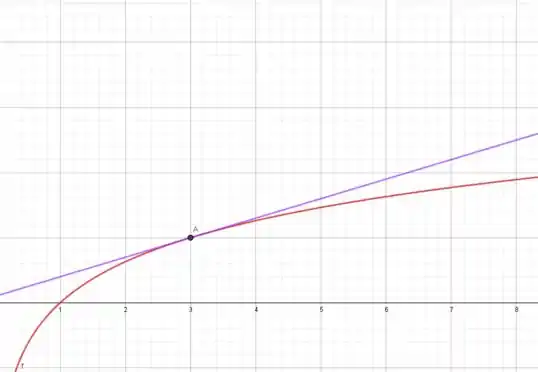
Veja que as funções se tornam indistinguíveis no ponto (3,1). Isso mostra que a linearização está correta.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Estime o volume do material presente em uma embalagem cilíndrica de 30 polegadas de altura, 6 polegadas de raio e 0,5 polegada de espessura.
O diâmetro de uma árvore era de 10 polegadas. No ano seguinte, a circunferência aumentou 2 polegadas. Qual foi a variação aproximada do diâmetro da árvore? E da área da seção transversal?
A quantidade de trabalho realizado pela principal câmara de bombeamento do coração, o ventrículo esquerdo, é dada pela equação W = P V + V δ v 2 2 g em que W é o trabalho por unidade de tempo, P é a p
O raio r de um círculo é medido com um erro de no máximo 2%. Qual é a porcentagem de erro máxima correspondente no cálculo da:a. circunferência do círculo? b. área do círculo?
Quando o comprimento L do pêndulo de um relógio é mantido constante por meio do controle de sua temperatura, o período T do pêndulo depende da aceleração g da gravidade. O período variará um pouco à m