Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 65

Um satélite gira em torno da terra numa órbita elíptica com excentricidade 1/3 e tendo a terra em um foco. A menor distância do satélite à terra é de 300 Km. Ache a maior distância entre o satélite e a terra.

Passo 1

Fazendo um esboço bem simples do sistema, é possivel perceber que a menor distância entre a órbita e um dos focos, no caso a Terra, fica justamente bem em cima de um

dos vértices.

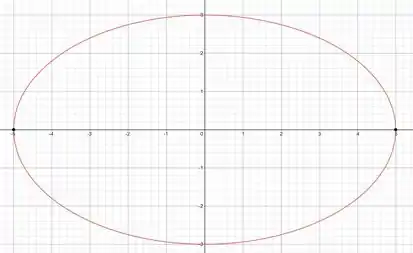
Pensando um pouco e observando o esboço no instante em que o satélite se encontra no vértice: a distância entre o centro do sistema e a Terra é c , a distância entre o centro do sistema e o satélite é a e a distância entre a terra e o sistema é 300 Km, logo podemos tomar a conclusão de que:

a = 300 + c

Passo 2

Lembrando um pouco das fórmulas, também sabemos que:

e = 1 3 = c a

Montando um sistema é possível descobrir o valor de a e de c :

1 3 = c a a = 300 + c ⟹ a = 3 c a = 300 + c ⟹ 3 c = 300 + c ⟹ c = 150

Agora descobrir o valor de a ficou fácil:

a = 3 c   ⟹   a = 3 × 150 ⟹       a = 450

Passo 3

Observando mais uma vez o esboço, percebe-se facilmente que a distância entre a terra e o outro vértice é:

d = c + a

d = 150 + 450

d = 600   k m

Resposta

d = 600   k m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a região limitada pelas duas parábolas: r = 2 ( 1 - cos ⁡ θ )er = 2 ( 1 + cos ⁡ θ )
Prove que o ponto médio de todas as cordas pararelas a uma corda fixa estão sobre uma reta pararela ao eixo da parábola.
Determine os pontos aos quais a curva r = 4 + 3 c o s ( θ ) tem retas tangentes horizontal e vertical. Faça um esboço gráfico com essas retas tangentes.
Mostre que x + y = a representa uma família monoparamétrica de de cônicas e determine o tipo da cônica. Faça um esboço do gráfico para a=1, a=2 e a=4.
Determine os pontos aos quais a curva r = 3 - 3 s e n ( θ ) tem retas tangentes horizontal e vertical. Faça um esboço gráfico com essas retas tangentes.