Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 51
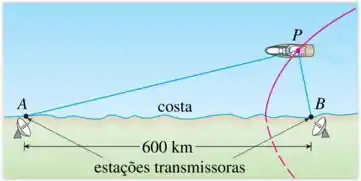
No sistema de navegação por rádio LORAN (LOng RAnge Navigation), duas estações locais de rádios situadas em e transmitem sinais simultaneamente para um navio ou avião localizados em . O computador de bordo converte a diferença de tempo na recepção desses sinais em diferença de distância e isso, de acordo com a definição de uma hipérbole, localiza o navio ou o avião em um ramo da hipérbole (veja a figura). Suponha que a estação esteja localizada a leste da estação na costa. Um navio recebe o sinal de microssegundos ) antes de receber o sinal de . (a) Assumindo que o sinal de rádio viaja a uma velocidade de , encontre uma equação da hipérbole na qual o navio está. (b) Se o navio deveria estar ao norte de , a que distância da costa ele estará?
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte figura que mostra um barco (ponto ) entre duas torres de estações de rádio e que transmitem simultaneamente sinais para esse barco:
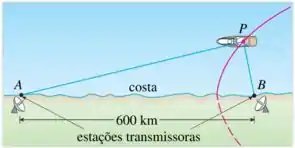
Suponha que a estação B esteja localizada 600 km a leste da estação A na costa. Um navio recebe o sinal B em 1200 μs antes de receber o sinal de A.
Primeira coisa vamos lembrar a equação geral da hipérbole
Na qual
Onde é a distância entre o centro da hipérbole e algum dos focos.
Outra coisa que seria interessante recordarmos, é que a dado um ponto qualquer em nossa hipérbole, a diferença entre a distância entre os focos e ponto, será sempre de .
Passo 2
- Na primeira parte do nosso problema, somos informados que a diferença entre o tempo que o sinal levou para o navio receber entre a estação e a foi de , ou seja
- Vamos tomar , teremos que:
Outra coisa que temos é que, como é a distância entre a origem e o foco, podemos observar que . Assim
Desta forma temos