Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 80
O sistema vascular sanguíneo consiste em vasos sanguíneos (artérias, arteríolas, capilares e veias) que transportam o sangue do coração para os órgãos e de volta para o coração. Esse sistema deve trabalhar de forma a minimizar a energia despendida pelo coração no bombeamento do sangue. Em particular, essa energia é reduzida quando a resistência do sangue diminui. Uma das Leis de Poiseuille dá a resistência do sangue como
onde é o comprimento do vaso sanguíneo; o raio; e é uma constante positiva determinada pela viscosidade do sangue. (Poiseuille estabeleceu essa lei experimentalmente, mas também seguiu a Equação 8.4.2.) A figura mostra um vaso sanguíneo principal de raio ramificado em um ângulo em um vaso menor de raio
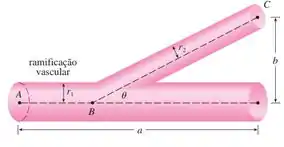
- Use a Lei de Poiseuille para mostrar que a resistência total do sangue ao longo do caminho é
- Demonstre que essa resistência é minimizada quando
- Encontre o ângulo ótimo de ramificação (com precisão de um grau) quando o raio do vaso sanguíneo menor é do raio do vaso maior.
onde e são as distâncias mostradas na figura.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dito que a resistência do sangue em uma artéria segue a função
A partir daí, queremos mostrar que para o sangue seguir o caminho na figura
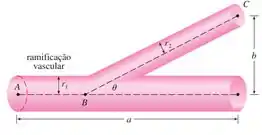
a resistência sofrida é dada por
Além disso, temos que mostrar que a resistência é minimizada se e também temos que encontrar o ângulo de ramificação quando o raio do vaso sanguíneo menor é do raio do vaso maior.
Parece complicado, não é?
Para responder o item a), temos que aplicar algumas relações trigonométricas na imagem da figura.
Para responder o item b), vamos aplicar o que aprendemos em máximos e mínimos de uma função... ou seja, vamos aplicar a derivada em em função de e igualar a .
E por último, vamos aplicar o resultado do item b) nas condições propostas no item c).
Sacou? Bora começar!
Passo 2
Criaremos um ponto para que o comprimento possa ser chamado de .
Pela figura, conseguimos fazer:
E também:
Igualando as duas equações temos:
A resistência total é:
Substituindo os valores de e , temos.
Tranquilo até aqui?
Passo 3
Minimizando a resistência, vamos derivar em função de
Pelo teorema fundamental do cálculo, temos que
Aplicando em ...
Para minimizar essa função, igualamos a , assim como fazemos para obter os pontos críticos de uma função...
Show?
Passo 4
Quando , substituindo na resposta do item anterior...
então,
E fim! O que achou? Responde Aí!
Resposta
(c)