Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 41
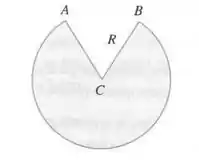
Um copo com formato cônico é feito de um pedaço circular de papel de raio cortando fora um setor e juntando os lados e . Encontre a capacidade máxima de tal copo.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a capacidade máxima de um copo, sabendo que ele foi feito em formato cônico, de um pedaço circular de papel, cortando fora um setor e juntando os lados e .
Esboçando a figura em três dimensões, teríamos isso aqui:
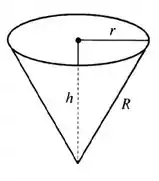
Como nós queremos saber a capacidade máxima desse cone, vamos usar a fórmula do volume do cone:
Depois vamos usar o triângulo retângulo formado na figura para isolar uma das variáveis e substituir na equação do volume . Assim, teremos dependendo apenas de uma das variáveis e poderemos encontrar os pontos de máximo da função.
Vamos lá!
Passo 2
O enunciado pede a capacidade máxima, ou seja, o volume, que tem a seguinte fórmula:
Essa fórmula está dependendo de duas variáveis, então, podemos usar o triângulo retângulo formado na figura acima para isolar uma delas:
Substituindo em , temos:
Passo 3
Agora a gente já pode maximizar a fórmula!! Aplicando a derivada:
E igualando o resultado a zero:
Isolando :
Já encontramos o valor de , que é o único ponto crítico da função e nosso ponto de máximo, agora é só substituir em :
E encontramos a capacidade máxima do copo.
Valeu, galera! Até a próxima! 😉